// @(#)root/geom:$Name: $:$Id: TGeoSphere.cxx,v 1.42 2005/05/13 16:20:38 brun Exp $
// Author: Andrei Gheata 31/01/02
// TGeoSphere::Contains() DistFromOutside/Out() implemented by Mihaela Gheata
/*************************************************************************
* Copyright (C) 1995-2000, Rene Brun and Fons Rademakers. *
* All rights reserved. *
* *
* For the licensing terms see $ROOTSYS/LICENSE. *
* For the list of contributors see $ROOTSYS/README/CREDITS. *
*************************************************************************/
//_____________________________________________________________________________
// TGeoSphere - spherical shell class. It takes 6 parameters :
// - inner and outer radius Rmin, Rmax
// - the theta limits Tmin, Tmax
// - the phi limits Pmin, Pmax (the sector in phi is considered
// starting from Pmin to Pmax counter-clockwise
//
//_____________________________________________________________________________
//
/*
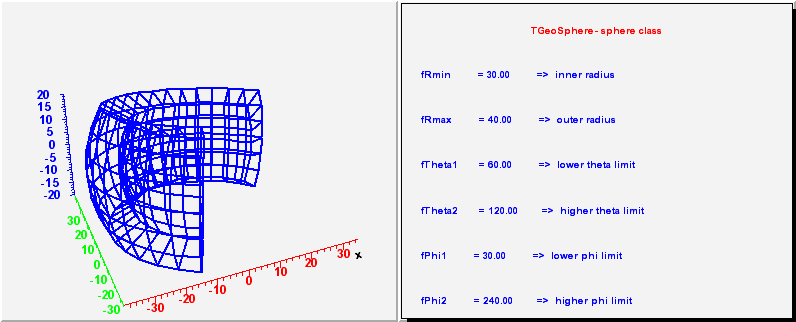 */
//
#include "Riostream.h"
#include "TROOT.h"
#include "TGeoCone.h"
#include "TGeoManager.h"
#include "TGeoVolume.h"
#include "TVirtualGeoPainter.h"
#include "TGeoSphere.h"
#include "TVirtualPad.h"
#include "TBuffer3D.h"
#include "TBuffer3DTypes.h"
ClassImp(TGeoSphere)
//_____________________________________________________________________________
TGeoSphere::TGeoSphere()
{
// Default constructor
SetShapeBit(TGeoShape::kGeoSph);
fNz = 0;
fNseg = 0;
fRmin = 0.0;
fRmax = 0.0;
fTheta1 = 0.0;
fTheta2 = 180.0;
fPhi1 = 0.0;
fPhi2 = 360.0;
}
//_____________________________________________________________________________
TGeoSphere::TGeoSphere(Double_t rmin, Double_t rmax, Double_t theta1,
Double_t theta2, Double_t phi1, Double_t phi2)
:TGeoBBox(0, 0, 0)
{
// Default constructor specifying minimum and maximum radius
SetShapeBit(TGeoShape::kGeoSph);
SetSphDimensions(rmin, rmax, theta1, theta2, phi1, phi2);
ComputeBBox();
SetNumberOfDivisions(20);
}
//_____________________________________________________________________________
TGeoSphere::TGeoSphere(const char *name, Double_t rmin, Double_t rmax, Double_t theta1,
Double_t theta2, Double_t phi1, Double_t phi2)
:TGeoBBox(name, 0, 0, 0)
{
// Default constructor specifying minimum and maximum radius
SetShapeBit(TGeoShape::kGeoSph);
SetSphDimensions(rmin, rmax, theta1, theta2, phi1, phi2);
ComputeBBox();
SetNumberOfDivisions(20);
}
//_____________________________________________________________________________
TGeoSphere::TGeoSphere(Double_t *param, Int_t /*nparam*/)
:TGeoBBox(0, 0, 0)
{
// Default constructor specifying minimum and maximum radius
// param[0] = Rmin
// param[1] = Rmax
SetShapeBit(TGeoShape::kGeoSph);
SetDimensions(param);
ComputeBBox();
SetNumberOfDivisions(20);
}
//_____________________________________________________________________________
TGeoSphere::~TGeoSphere()
{
// destructor
}
//_____________________________________________________________________________
void TGeoSphere::ComputeBBox()
{
// compute bounding box of the sphere
// Double_t xmin, xmax, ymin, ymax, zmin, zmax;
if (TMath::Abs(fTheta2-fTheta1) == 180) {
if (TMath::Abs(fPhi2-fPhi1) == 360) {
TGeoBBox::SetBoxDimensions(fRmax, fRmax, fRmax);
memset(fOrigin, 0, 3*sizeof(Double_t));
return;
}
}
Double_t st1 = TMath::Sin(fTheta1*TMath::DegToRad());
Double_t st2 = TMath::Sin(fTheta2*TMath::DegToRad());
Double_t r1min, r1max, r2min, r2max, rmin, rmax;
r1min = TMath::Min(fRmax*st1, fRmax*st2);
r1max = TMath::Max(fRmax*st1, fRmax*st2);
r2min = TMath::Min(fRmin*st1, fRmin*st2);
r2max = TMath::Max(fRmin*st1, fRmin*st2);
if (((fTheta1<=90) && (fTheta2>=90)) || ((fTheta2<=90) && (fTheta1>=90))) {
r1max = fRmax;
r2max = fRmin;
}
rmin = TMath::Min(r1min, r2min);
rmax = TMath::Max(r1max, r2max);
Double_t xc[4];
Double_t yc[4];
xc[0] = rmax*TMath::Cos(fPhi1*TMath::DegToRad());
yc[0] = rmax*TMath::Sin(fPhi1*TMath::DegToRad());
xc[1] = rmax*TMath::Cos(fPhi2*TMath::DegToRad());
yc[1] = rmax*TMath::Sin(fPhi2*TMath::DegToRad());
xc[2] = rmin*TMath::Cos(fPhi1*TMath::DegToRad());
yc[2] = rmin*TMath::Sin(fPhi1*TMath::DegToRad());
xc[3] = rmin*TMath::Cos(fPhi2*TMath::DegToRad());
yc[3] = rmin*TMath::Sin(fPhi2*TMath::DegToRad());
Double_t xmin = xc[TMath::LocMin(4, &xc[0])];
Double_t xmax = xc[TMath::LocMax(4, &xc[0])];
Double_t ymin = yc[TMath::LocMin(4, &yc[0])];
Double_t ymax = yc[TMath::LocMax(4, &yc[0])];
Double_t dp = fPhi2-fPhi1;
if (dp<0) dp+=360;
Double_t ddp = -fPhi1;
if (ddp<0) ddp+= 360;
if (ddp>360) ddp-=360;
if (ddp<=dp) xmax = rmax;
ddp = 90-fPhi1;
if (ddp<0) ddp+= 360;
if (ddp>360) ddp-=360;
if (ddp<=dp) ymax = rmax;
ddp = 180-fPhi1;
if (ddp<0) ddp+= 360;
if (ddp>360) ddp-=360;
if (ddp<=dp) xmin = -rmax;
ddp = 270-fPhi1;
if (ddp<0) ddp+= 360;
if (ddp>360) ddp-=360;
if (ddp<=dp) ymin = -rmax;
xc[0] = fRmax*TMath::Cos(fTheta1*TMath::DegToRad());
xc[1] = fRmax*TMath::Cos(fTheta2*TMath::DegToRad());
xc[2] = fRmin*TMath::Cos(fTheta1*TMath::DegToRad());
xc[3] = fRmin*TMath::Cos(fTheta2*TMath::DegToRad());
Double_t zmin = xc[TMath::LocMin(4, &xc[0])];
Double_t zmax = xc[TMath::LocMax(4, &xc[0])];
fOrigin[0] = (xmax+xmin)/2;
fOrigin[1] = (ymax+ymin)/2;
fOrigin[2] = (zmax+zmin)/2;;
fDX = (xmax-xmin)/2;
fDY = (ymax-ymin)/2;
fDZ = (zmax-zmin)/2;
}
//_____________________________________________________________________________
void TGeoSphere::ComputeNormal(Double_t *point, Double_t *dir, Double_t *norm)
{
// Compute normal to closest surface from POINT.
Double_t rxy2 = point[0]*point[0]+point[1]*point[1];
Double_t r2 = rxy2+point[2]*point[2];
Double_t r=TMath::Sqrt(r2);
Bool_t rzero=kFALSE;
if (r<=1E-20) rzero=kTRUE;
//localize theta
Double_t phi=0;
Double_t th=0.;
if (!rzero) th = TMath::ACos(point[2]/r);
//localize phi
phi=TMath::ATan2(point[1], point[0]);
Double_t saf[4];
saf[0]=(fRmin==0 && !TestShapeBit(kGeoThetaSeg) && !TestShapeBit(kGeoPhiSeg))?TGeoShape::Big():TMath::Abs(r-fRmin);
saf[1]=TMath::Abs(fRmax-r);
saf[2]=saf[3]= TGeoShape::Big();
if (TestShapeBit(kGeoThetaSeg)) {
if (fTheta1>0) {
saf[2] = r*TMath::Abs(TMath::Sin(th-fTheta1*TMath::DegToRad()));
}
if (fTheta2<180) {
saf[3] = r*TMath::Abs(TMath::Sin(fTheta2*TMath::DegToRad()-th));
}
}
Int_t i = TMath::LocMin(4,saf);
if (TestShapeBit(kGeoPhiSeg)) {
Double_t c1 = TMath::Cos(fPhi1*TMath::DegToRad());
Double_t s1 = TMath::Sin(fPhi1*TMath::DegToRad());
Double_t c2 = TMath::Cos(fPhi2*TMath::DegToRad());
Double_t s2 = TMath::Sin(fPhi2*TMath::DegToRad());
if (TGeoShape::IsCloseToPhi(saf[i], point,c1,s1,c2,s2)) {
TGeoShape::NormalPhi(point,dir,norm,c1,s1,c2,s2);
return;
}
}
if (i>1) {
if (i==2) th=(fTheta1<90)?(fTheta1+90):(fTheta1-90);
else th=(fTheta2<90)?(fTheta2+90):(fTheta2-90);
th *= TMath::DegToRad();
}
norm[0] = TMath::Sin(th)*TMath::Cos(phi);
norm[1] = TMath::Sin(th)*TMath::Sin(phi);
norm[2] = TMath::Cos(th);
if (norm[0]*dir[0]+norm[1]*dir[1]+norm[2]*dir[2]<0) {
norm[0] = -norm[0];
norm[1] = -norm[1];
norm[2] = -norm[2];
}
}
//_____________________________________________________________________________
Bool_t TGeoSphere::IsPointInside(Double_t *point, Bool_t checkR, Bool_t checkTh, Bool_t checkPh) const
{
Double_t r2 = point[0]*point[0]+point[1]*point[1]+point[2]*point[2];
if (checkR) {
if (TestShapeBit(kGeoRSeg) && (r2<fRmin*fRmin)) return kFALSE;
if (r2>fRmax*fRmax) return kFALSE;
}
if (r2<1E-20) return kTRUE;
if (checkPh && TestShapeBit(kGeoPhiSeg)) {
Double_t phi = TMath::ATan2(point[1], point[0]) * TMath::RadToDeg();
while (phi < fPhi1) phi+=360.;
Double_t dphi = fPhi2 -fPhi1;
Double_t ddp = phi - fPhi1;
if (ddp > dphi) return kFALSE;
}
if (checkTh && TestShapeBit(kGeoThetaSeg)) {
r2=TMath::Sqrt(r2);
// check theta range
Double_t theta = TMath::ACos(point[2]/r2)*TMath::RadToDeg();
if ((theta<fTheta1) || (theta>fTheta2)) return kFALSE;
}
return kTRUE;
}
//_____________________________________________________________________________
Bool_t TGeoSphere::Contains(Double_t *point) const
{
// test if point is inside this sphere
// check Rmin<=R<=Rmax
Double_t r2=point[0]*point[0]+point[1]*point[1]+point[2]*point[2];
if (TestShapeBit(kGeoRSeg) && (r2<fRmin*fRmin)) return kFALSE;
if (r2>fRmax*fRmax) return kFALSE;
if (r2<1E-20) return kTRUE;
// check phi range
if (TestShapeBit(kGeoPhiSeg)) {
Double_t phi = TMath::ATan2(point[1], point[0]) * TMath::RadToDeg();
if (phi < 0 ) phi+=360.;
Double_t dphi = fPhi2 -fPhi1;
if (dphi < 0) dphi+=360.;
Double_t ddp = phi - fPhi1;
if (ddp < 0) ddp += 360.;
if (ddp > dphi) return kFALSE;
}
if (TestShapeBit(kGeoThetaSeg)) {
r2=TMath::Sqrt(r2);
// check theta range
Double_t theta = TMath::ACos(point[2]/r2)*TMath::RadToDeg();
if ((theta<fTheta1) || (theta>fTheta2)) return kFALSE;
}
return kTRUE;
}
//_____________________________________________________________________________
Int_t TGeoSphere::DistancetoPrimitive(Int_t px, Int_t py)
{
// compute closest distance from point px,py to each corner
Int_t n = fNseg+1;
Int_t nz = fNz+1;
const Int_t numPoints = 2*n*nz;
return ShapeDistancetoPrimitive(numPoints, px, py);
}
//_____________________________________________________________________________
Double_t TGeoSphere::DistFromOutside(Double_t *point, Double_t *dir, Int_t iact, Double_t step, Double_t *safe) const
{
// compute distance from outside point to surface of the sphere
Double_t saf[6];
Double_t rxy2 = point[0]*point[0]+point[1]*point[1];
Double_t rxy = TMath::Sqrt(rxy2);
Double_t r2 = rxy2+point[2]*point[2];
Double_t r=TMath::Sqrt(r2);
Bool_t rzero=kFALSE;
Double_t phi=0;;
if (r<1E-20) rzero=kTRUE;
//localize theta
Double_t th=0.;
if (TestShapeBit(kGeoThetaSeg) && (!rzero)) {
th = TMath::ACos(point[2]/r)*TMath::RadToDeg();
}
//localize phi
if (TestShapeBit(kGeoPhiSeg)) {
phi=TMath::ATan2(point[1], point[0])*TMath::RadToDeg();
if (phi<0) phi+=360.;
}
if (iact<3 && safe) {
saf[0]=(r<fRmin)?fRmin-r:TGeoShape::Big();
saf[1]=(r>fRmax)?(r-fRmax):TGeoShape::Big();
saf[2]=saf[3]=saf[4]=saf[5]= TGeoShape::Big();
if (TestShapeBit(kGeoThetaSeg)) {
if (th < fTheta1) {
saf[2] = r*TMath::Sin((fTheta1-th)*TMath::DegToRad());
}
if (th > fTheta2) {
saf[3] = r*TMath::Sin((th-fTheta2)*TMath::DegToRad());
}
}
if (TestShapeBit(kGeoPhiSeg)) {
Double_t dph1=phi-fPhi1;
if (dph1<0) dph1+=360.;
if (dph1<=90.) saf[4]=rxy*TMath::Sin(dph1*TMath::DegToRad());
Double_t dph2=fPhi2-phi;
if (dph2<0) dph2+=360.;
if (dph2>90.) saf[5]=rxy*TMath::Sin(dph2*TMath::DegToRad());
}
*safe = saf[TMath::LocMin(6, &saf[0])];
if (iact==0) return TGeoShape::Big();
if (iact==1 && step<*safe) return TGeoShape::Big();
}
// compute distance to shape
Double_t snxt = TGeoShape::Big();
Double_t rdotn = point[0]*dir[0]+point[1]*dir[1]+point[2]*dir[2];
Bool_t fullsph = (!TestShapeBit(kGeoThetaSeg) && !TestShapeBit(kGeoPhiSeg))?kTRUE:kFALSE;
if (fullsph) {
Bool_t inrmax = kFALSE;
Bool_t inrmin = kFALSE;
if (r<=fRmax+TGeoShape::Tolerance()) inrmax = kTRUE;
if (r>=fRmin-TGeoShape::Tolerance()) inrmin = kTRUE;
if (inrmax && inrmin) {
if ((fRmax-r) < (r-fRmin)) {
// close to Rmax
if (rdotn>=0) return TGeoShape::Big();
return 0.0; // already in
}
// close to Rmin
if (fRmin==0.0 || rdotn>=0) return 0.0;
// check second crossing of Rmin
return DistToSphere(point, dir, fRmin, kFALSE, kFALSE);
}
}
// first check if any crossing at all
if (r>fRmax) {
Double_t b = rdotn;
Double_t c = r2-fRmax*fRmax;
Double_t d=b*b-c;
if (d<0) return TGeoShape::Big();
}
// do rmin, rmax, checking phi and theta ranges
if (r<fRmin) {
// check first cross of rmin
snxt = DistToSphere(point, dir, fRmin, kTRUE);
if (snxt<1E20) return snxt;
} else {
if (r>fRmax) {
// point outside rmax, check first cross of rmax
snxt = DistToSphere(point, dir, fRmax, kTRUE);
if (snxt<1E20) return snxt;
// now check first crossing of rmin
if (fRmin>0) {
snxt = DistToSphere(point, dir, fRmin, kTRUE);
// if this is outside range, check second crossing of rmin
if (snxt>1E20) {
snxt = DistToSphere(point, dir, fRmin, kTRUE, kFALSE);
if (snxt<1E20) return snxt;
}
}
} else {
// point between rmin and rmax, check first cross of rmin
snxt = DistToSphere(point, dir, fRmin, kTRUE);
// if this is outside range, check second crossing of rmin
if (snxt>1E20) {
snxt = DistToSphere(point, dir, fRmin, kTRUE, kFALSE);
if (snxt<1E20) return snxt;
}
}
}
// check theta conical surfaces
Double_t ptnew[3];
Double_t b,delta, znew;
Double_t st1=TGeoShape::Big(), st2=TGeoShape::Big();
if (TestShapeBit(kGeoThetaSeg)) {
if (fTheta1>0) {
if (fTheta1==90) {
// surface is a plane
if (point[2]*dir[2]<0) {
snxt = -point[2]/dir[2];
ptnew[0] = point[0]+snxt*dir[0];
ptnew[1] = point[1]+snxt*dir[1];
ptnew[2] = 0;
// check range
if (IsPointInside(&ptnew[0], kTRUE, kFALSE, kTRUE)) return snxt;
}
} else {
Double_t r1,r2,z1,z2,dz;
Double_t si = TMath::Sin(fTheta1*TMath::DegToRad());
Double_t ci = TMath::Cos(fTheta1*TMath::DegToRad());
if (ci>0) {
r1 = fRmin*si;
z1 = fRmin*ci;
r2 = fRmax*si;
z2 = fRmax*ci;
} else {
r1 = fRmax*si;
z1 = fRmax*ci;
r2 = fRmin*si;
z2 = fRmin*ci;
}
dz = 0.5*(z2-z1);
ptnew[0] = point[0];
ptnew[1] = point[1];
ptnew[2] = point[2]-0.5*(z1+z2);
if (TestShapeBit(kGeoPhiSeg)) {
st1 = TGeoConeSeg::DistToCons(point, dir, r1, z1, r2, z2, fPhi1, fPhi2);
} else {
TGeoCone::DistToCone(ptnew, dir, dz, r1, r2, b, delta);
if (delta>0) {
st1 = -b-delta;
znew = ptnew[2]+st1*dir[2];
if (st1<0 || TMath::Abs(znew)>0) {
st1 = -b+delta;
znew = ptnew[2]+st1*dir[2];
if (st1<0 || TMath::Abs(znew)>0) st1=TGeoShape::Big();
}
}
}
}
}
if (fTheta2<180) {
if (fTheta2==90) {
// surface is a plane
if (point[2]*dir[2]<0) {
snxt = -point[2]/dir[2];
ptnew[0] = point[0]+snxt*dir[0];
ptnew[1] = point[1]+snxt*dir[1];
ptnew[2] = 0;
// check range
if (IsPointInside(&ptnew[0], kTRUE, kFALSE, kTRUE)) return snxt;
}
} else {
Double_t r1,r2,z1,z2,dz;
Double_t si = TMath::Sin(fTheta2*TMath::DegToRad());
Double_t ci = TMath::Cos(fTheta2*TMath::DegToRad());
if (ci>0) {
r1 = fRmin*si;
z1 = fRmin*ci;
r2 = fRmax*si;
z2 = fRmax*ci;
} else {
r1 = fRmax*si;
z1 = fRmax*ci;
r2 = fRmin*si;
z2 = fRmin*ci;
}
dz = 0.5*(z2-z1);
ptnew[0] = point[0];
ptnew[1] = point[1];
ptnew[2] = point[2]-0.5*(z1+z2);
if (TestShapeBit(kGeoPhiSeg)) {
st2 = TGeoConeSeg::DistToCons(point, dir, r1, z1, r2, z2, fPhi1, fPhi2);
} else {
TGeoCone::DistToCone(ptnew, dir, dz, r1, r2, b, delta);
if (delta>0) {
st2 = -b-delta;
znew = ptnew[2]+st2*dir[2];
if (st2<0 || TMath::Abs(znew)>dz) {
st2 = -b+delta;
znew = ptnew[2]+st2*dir[2];
if (st2<0 || TMath::Abs(znew)>0) st2=TGeoShape::Big();
}
}
}
}
}
}
snxt = TMath::Min(st1, st2);
// if (snxt<1E20) return snxt;
if (TestShapeBit(kGeoPhiSeg)) {
Double_t s1 = TMath::Sin(fPhi1*TMath::DegToRad());
Double_t c1 = TMath::Cos(fPhi1*TMath::DegToRad());
Double_t s2 = TMath::Sin(fPhi2*TMath::DegToRad());
Double_t c2 = TMath::Cos(fPhi2*TMath::DegToRad());
Double_t phim = 0.5*(fPhi1+fPhi2);
Double_t sm = TMath::Sin(phim*TMath::DegToRad());
Double_t cm = TMath::Cos(phim*TMath::DegToRad());
Double_t sfi1=TGeoShape::Big();
Double_t sfi2=TGeoShape::Big();
Double_t s=0;
Double_t safety, un;
safety = point[0]*s1-point[1]*c1;
if (safety>0) {
un = dir[0]*s1-dir[1]*c1;
if (un<0) {
s=-safety/un;
ptnew[0] = point[0]+s*dir[0];
ptnew[1] = point[1]+s*dir[1];
ptnew[2] = point[2]+s*dir[2];
if ((ptnew[1]*cm-ptnew[0]*sm)<=0) {
sfi1=s;
if (IsPointInside(&ptnew[0], kTRUE, kTRUE, kFALSE) && sfi1<snxt) return sfi1;
}
}
}
safety = -point[0]*s2+point[1]*c2;
if (safety>0) {
un = -dir[0]*s2+dir[1]*c2;
if (un<0) {
s=-safety/un;
ptnew[0] = point[0]+s*dir[0];
ptnew[1] = point[1]+s*dir[1];
ptnew[2] = point[2]+s*dir[2];
if ((ptnew[1]*cm-ptnew[0]*sm)>=0) {
sfi2=s;
if (IsPointInside(&ptnew[0], kTRUE, kTRUE, kFALSE) && sfi2<snxt) return sfi2;
}
}
}
}
return snxt;
}
//_____________________________________________________________________________
Double_t TGeoSphere::DistFromInside(Double_t *point, Double_t *dir, Int_t iact, Double_t step, Double_t *safe) const
{
// compute distance from inside point to surface of the sphere
Double_t saf[6];
Double_t rxy2 = point[0]*point[0]+point[1]*point[1];
Double_t rxy = TMath::Sqrt(rxy2);
Double_t r2 = rxy2+point[2]*point[2];
Double_t r=TMath::Sqrt(r2);
Bool_t rzero=kFALSE;
if (r<=1E-20) rzero=kTRUE;
//localize theta
Double_t phi=0;;
Double_t th=0.;
if (TestShapeBit(kGeoThetaSeg) && (!rzero)) {
th = TMath::ACos(point[2]/r)*TMath::RadToDeg();
}
//localize phi
if (TestShapeBit(kGeoPhiSeg)) {
phi=TMath::ATan2(point[1], point[0])*TMath::RadToDeg();
if (phi<0) phi+=360.;
}
if (iact<3 && safe) {
saf[0]=(fRmin==0)?TGeoShape::Big():r-fRmin;
saf[1]=fRmax-r;
saf[2]=saf[3]=saf[4]=saf[5]= TGeoShape::Big();
if (TestShapeBit(kGeoThetaSeg)) {
if (fTheta1>0) {
saf[2] = r*TMath::Sin((th-fTheta1)*TMath::DegToRad());
}
if (fTheta2<180) {
saf[3] = r*TMath::Sin((fTheta2-th)*TMath::DegToRad());
}
}
if (TestShapeBit(kGeoPhiSeg)) {
Double_t dph1=phi-fPhi1;
if (dph1<0) dph1+=360.;
if (dph1<=90.) saf[4]=rxy*TMath::Sin(dph1*TMath::DegToRad());
Double_t dph2=fPhi2-phi;
if (dph2<0) dph2+=360.;
if (dph2<=90.) saf[5]=rxy*TMath::Sin(dph2*TMath::DegToRad());
}
*safe = saf[TMath::LocMin(6, &saf[0])];
if (iact==0) return TGeoShape::Big();
if (iact==1 && step<*safe) return TGeoShape::Big();
}
// compute distance to shape
Double_t snxt = TGeoShape::Big();
if (rzero) {
// gGeoManager->SetNormalChecked(1.);
return fRmax;
}
// first do rmin, rmax
Double_t b,delta, znew;
Double_t rdotn = point[0]*dir[0]+point[1]*dir[1]+point[2]*dir[2];
Double_t sn1 = TGeoShape::Big();
// Inner sphere
if (fRmin>0) {
// Protection in case point is actually outside the sphere
if (r <= fRmin+TGeoShape::Tolerance()) {
if (rdotn<0) return 0.0;
} else {
if (rdotn<0) sn1 = DistToSphere(point, dir, fRmin, kFALSE);
}
}
Double_t sn2 = TGeoShape::Big();
// Outer sphere
if (r >= fRmax-TGeoShape::Tolerance()) {
if (rdotn>=0) return 0.0;
}
sn2 = DistToSphere(point, dir, fRmax, kFALSE);
Double_t sr = TMath::Min(sn1, sn2);
// check theta conical surfaces
sn1 = TGeoShape::Big();
sn2 = TGeoShape::Big();
if (TestShapeBit(kGeoThetaSeg)) {
if (fTheta1==90) {
// surface is a plane
if (point[2]*dir[2]<0) sn1 = -point[2]/dir[2];
} else {
if (fTheta1>0) {
Double_t r1,r2,z1,z2,dz,ptnew[3];
Double_t si = TMath::Sin(fTheta1*TMath::DegToRad());
Double_t ci = TMath::Cos(fTheta1*TMath::DegToRad());
if (ci>0) {
r1 = fRmin*si;
z1 = fRmin*ci;
r2 = fRmax*si;
z2 = fRmax*ci;
} else {
r1 = fRmax*si;
z1 = fRmax*ci;
r2 = fRmin*si;
z2 = fRmin*ci;
}
dz = 0.5*(z2-z1);
ptnew[0] = point[0];
ptnew[1] = point[1];
ptnew[2] = point[2]-0.5*(z1+z2);
if (TestShapeBit(kGeoPhiSeg)) {
sn1 = TGeoConeSeg::DistToCons(point, dir, r1, z1, r2, z2, fPhi1, fPhi2);
} else {
TGeoCone::DistToCone(ptnew, dir, dz, r1, r2, b, delta);
if (delta>0) {
sn1 = -b-delta;
znew = ptnew[2]+sn1*dir[2];
if (sn1<0 || TMath::Abs(znew)>dz) {
sn1 = -b+delta;
znew = ptnew[2]+sn1*dir[2];
if (sn1<0 || TMath::Abs(znew)>0) sn1=TGeoShape::Big();
}
}
}
}
}
if (fTheta2==90) {
// surface is a plane
if (point[2]*dir[2]<0) sn1 = -point[2]/dir[2];
} else {
if (fTheta2<180) {
Double_t r1,r2,z1,z2,dz,ptnew[3];
Double_t si = TMath::Sin(fTheta2*TMath::DegToRad());
Double_t ci = TMath::Cos(fTheta2*TMath::DegToRad());
if (ci>0) {
r1 = fRmin*si;
z1 = fRmin*ci;
r2 = fRmax*si;
z2 = fRmax*ci;
} else {
r1 = fRmax*si;
z1 = fRmax*ci;
r2 = fRmin*si;
z2 = fRmin*ci;
}
dz = 0.5*(z2-z1);
ptnew[0] = point[0];
ptnew[1] = point[1];
ptnew[2] = point[2]-0.5*(z1+z2);
if (TestShapeBit(kGeoPhiSeg)) {
sn2 = TGeoConeSeg::DistToCons(point, dir, r1, z1, r2, z2, fPhi1, fPhi2);
} else {
TGeoCone::DistToCone(ptnew, dir, dz, r1, r2, b, delta);
if (delta>0) {
sn2 = -b-delta;
znew = ptnew[2]+sn2*dir[2];
if (sn2<0 || TMath::Abs(znew)>0) {
sn2 = -b+delta;
znew = ptnew[2]+sn2*dir[2];
if (sn2<0 || TMath::Abs(znew)>0) sn2=TGeoShape::Big();
}
}
}
}
}
}
Double_t st = TMath::Min(sn1,sn2);
Double_t sp = TGeoShape::Big();
if (TestShapeBit(kGeoPhiSeg)) {
Double_t s1 = TMath::Sin(fPhi1*TMath::DegToRad());
Double_t c1 = TMath::Cos(fPhi1*TMath::DegToRad());
Double_t s2 = TMath::Sin(fPhi2*TMath::DegToRad());
Double_t c2 = TMath::Cos(fPhi2*TMath::DegToRad());
Double_t phim = 0.5*(fPhi1+fPhi2);
Double_t sm = TMath::Sin(phim*TMath::DegToRad());
Double_t cm = TMath::Cos(phim*TMath::DegToRad());
sp = TGeoShape::DistToPhiMin(point, dir, s1, c1, s2, c2, sm, cm);
}
snxt = TMath::Min(sr, st);
snxt = TMath::Min(snxt, sp);
return snxt;
}
//_____________________________________________________________________________
Double_t TGeoSphere::DistToSphere(Double_t *point, Double_t *dir, Double_t rsph, Bool_t check, Bool_t firstcross) const
{
// compute distance to sphere of radius rsph. Direction has to be a unit vector
if (rsph<=0) return TGeoShape::Big();
Double_t s=TGeoShape::Big();
Double_t r2 = point[0]*point[0]+point[1]*point[1]+point[2]*point[2];
Double_t b = point[0]*dir[0]+point[1]*dir[1]+point[2]*dir[2];
Double_t c = r2-rsph*rsph;
Bool_t in = (c<=0)?kTRUE:kFALSE;
Double_t d;
d=b*b-c;
if (d<0) return TGeoShape::Big();
Double_t pt[3];
Int_t i;
d = TMath::Sqrt(d);
if (in) {
s=-b+d;
} else {
s = (firstcross)?(-b-d):(-b+d);
}
if (s<0) return TGeoShape::Big();
if (!check) return s;
for (i=0; i<3; i++) pt[i]=point[i]+s*dir[i];
// check theta and phi ranges
if (IsPointInside(&pt[0], kFALSE)) return s;
return TGeoShape::Big();
}
//_____________________________________________________________________________
TGeoVolume *TGeoSphere::Divide(TGeoVolume * /*voldiv*/, const char * /*divname*/, Int_t /*iaxis*/, Int_t /*ndiv*/,
Double_t /*start*/, Double_t /*step*/)
{
// Divide all range of iaxis in range/step cells
Error("Divide", "Division of a sphere not implemented");
return 0;
}
//_____________________________________________________________________________
const char *TGeoSphere::GetAxisName(Int_t iaxis) const
{
// Returns name of axis IAXIS.
switch (iaxis) {
case 1:
return "R";
case 2:
return "THETA";
case 3:
return "PHI";
default:
return "UNDEFINED";
}
}
//_____________________________________________________________________________
Double_t TGeoSphere::GetAxisRange(Int_t iaxis, Double_t &xlo, Double_t &xhi) const
{
// Get range of shape for a given axis.
xlo = 0;
xhi = 0;
Double_t dx = 0;
switch (iaxis) {
case 1:
xlo = fRmin;
xhi = fRmax;
dx = xhi-xlo;
return dx;
case 2:
xlo = fPhi1;
xhi = fPhi2;
dx = xhi-xlo;
return dx;
case 3:
xlo = fTheta1;
xhi = fTheta2;
dx = xhi-xlo;
return dx;
}
return dx;
}
//_____________________________________________________________________________
void TGeoSphere::GetBoundingCylinder(Double_t *param) const
{
//--- Fill vector param[4] with the bounding cylinder parameters. The order
// is the following : Rmin, Rmax, Phi1, Phi2
Double_t smin = TMath::Sin(fTheta1*TMath::DegToRad());
Double_t smax = TMath::Sin(fTheta2*TMath::DegToRad());
if (smin>smax) {
Double_t a = smin;
smin = smax;
smax = a;
}
param[0] = fRmin*smin; // Rmin
param[0] *= param[0];
if (((90.-fTheta1)*(fTheta2-90.))>=0) smax = 1.;
param[1] = fRmax*smax; // Rmax
param[1] *= param[1];
param[2] = (fPhi1<0)?(fPhi1+360.):fPhi1; // Phi1
param[3] = fPhi2;
if ((param[3]-param[2])==360.) { // Phi2
param[2] = 0.;
param[3] = 360.;
}
while (param[3]<param[2]) param[3]+=360.;
}
//_____________________________________________________________________________
void TGeoSphere::InspectShape() const
{
// print shape parameters
printf("*** Shape %s: TGeoSphere ***\n", GetName());
printf(" Rmin = %11.5f\n", fRmin);
printf(" Rmax = %11.5f\n", fRmax);
printf(" Th1 = %11.5f\n", fTheta1);
printf(" Th2 = %11.5f\n", fTheta2);
printf(" Ph1 = %11.5f\n", fPhi1);
printf(" Ph2 = %11.5f\n", fPhi2);
printf(" Bounding box:\n");
TGeoBBox::InspectShape();
}
//_____________________________________________________________________________
TBuffer3D *TGeoSphere::MakeBuffer3D() const
{
// Creates a TBuffer3D describing *this* shape.
// Coordinates are in local reference frame.
Int_t n = gGeoManager->GetNsegments()+1;
Double_t ph1 = GetPhi1();
Double_t ph2 = GetPhi2();
Int_t nz = GetNz()+1;
if (nz < 2) return 0;
Int_t NbPnts = 2*n*nz;
if (NbPnts <= 0) return 0;
Bool_t specialCase = kFALSE;
if (TMath::Abs(TMath::Sin(2*(ph2 - ph1))) <= 0.01) specialCase = kTRUE;
Int_t NbSegs = 4*(nz*n-1+(specialCase == kTRUE));
Int_t NbPols = 2*(nz*n-1+(specialCase == kTRUE));
TBuffer3D* buff = new TBuffer3D(TBuffer3DTypes::kGeneric,
NbPnts, 3*NbPnts, NbSegs, 3*NbSegs, NbPols, 6*NbPols);
if (buff)
{
SetPoints(buff->fPnts);
SetSegsAndPols(*buff);
}
return buff;
}
//_____________________________________________________________________________
void TGeoSphere::SetSegsAndPols(TBuffer3D & buff) const
{
// Fill TBuffer3D structure for segments and polygons.
Int_t i, j;
Int_t n = gGeoManager->GetNsegments()+1;
Double_t ph1 = GetPhi1();
Double_t ph2 = GetPhi2();
Int_t nz = GetNz()+1;
if (nz < 2) return;
Bool_t specialCase = kFALSE;
if (TMath::Abs(TMath::Sin(2*(ph2 - ph1))) <= 0.01) specialCase = kTRUE;
Int_t c = GetBasicColor();
Int_t indx, indx2, k;
indx = indx2 = 0;
//inside & outside spheres, number of segments: 2*nz*(n-1)
// special case number of segments: 2*nz*n
for (i = 0; i < nz*2; i++) {
indx2 = i*n;
for (j = 1; j < n; j++) {
buff.fSegs[indx++] = c;
buff.fSegs[indx++] = indx2+j-1;
buff.fSegs[indx++] = indx2+j;
}
if (specialCase) {
buff.fSegs[indx++] = c;
buff.fSegs[indx++] = indx2+j-1;
buff.fSegs[indx++] = indx2;
}
}
//bottom & top lines, number of segments: 2*n
for (i = 0; i < 2; i++) {
indx2 = i*(nz-1)*2*n;
for (j = 0; j < n; j++) {
buff.fSegs[indx++] = c;
buff.fSegs[indx++] = indx2+j;
buff.fSegs[indx++] = indx2+n+j;
}
}
//inside & outside spheres, number of segments: 2*(nz-1)*n
for (i = 0; i < (nz-1); i++) {
//inside sphere
indx2 = i*n*2;
for (j = 0; j < n; j++) {
buff.fSegs[indx++] = c+2;
buff.fSegs[indx++] = indx2+j;
buff.fSegs[indx++] = indx2+n*2+j;
}
//outside sphere
indx2 = i*n*2+n;
for (j = 0; j < n; j++) {
buff.fSegs[indx++] = c+3;
buff.fSegs[indx++] = indx2+j;
buff.fSegs[indx++] = indx2+n*2+j;
}
}
//left & right sections, number of segments: 2*(nz-2)
// special case number of segments: 0
if (!specialCase) {
for (i = 1; i < (nz-1); i++) {
for (j = 0; j < 2; j++) {
buff.fSegs[indx++] = c;
buff.fSegs[indx++] = 2*i * n + j*(n-1);
buff.fSegs[indx++] = (2*i+1) * n + j*(n-1);
}
}
}
Int_t m = n - 1 + (specialCase == kTRUE);
indx = 0;
//bottom & top, number of polygons: 2*(n-1)
// special case number of polygons: 2*n
i = 0;
for (j = 0; j < n-1; j++) {
buff.fPols[indx++] = c+3;
buff.fPols[indx++] = 4;
buff.fPols[indx++] = i*(nz*2-2)*m+j;
buff.fPols[indx++] = 2*nz*m+i*n+j+1;
buff.fPols[indx++] = i*(nz*2-2)*m+m+j;
buff.fPols[indx++] = 2*nz*m+i*n+j;
}
if (specialCase) {
buff.fPols[indx++] = c+3;
buff.fPols[indx++] = 4;
buff.fPols[indx++] = i*(nz*2-2)*m+j;
buff.fPols[indx++] = 2*nz*m+i*n;
buff.fPols[indx++] = i*(nz*2-2)*m+m+j;
buff.fPols[indx++] = 2*nz*m+i*n+j;
}
i = 1;
for (j = 0; j < n-1; j++) {
buff.fPols[indx++] = c+3;
buff.fPols[indx++] = 4;
buff.fPols[indx++] = 2*nz*m+i*n+j;
buff.fPols[indx++] = i*(nz*2-2)*m+m+j;
buff.fPols[indx++] = 2*nz*m+i*n+j+1;
buff.fPols[indx++] = i*(nz*2-2)*m+j;
}
if (specialCase) {
buff.fPols[indx++] = c+3;
buff.fPols[indx++] = 4;
buff.fPols[indx++] = 2*nz*m+i*n+j;
buff.fPols[indx++] = i*(nz*2-2)*m+m+j;
buff.fPols[indx++] = 2*nz*m+i*n;
buff.fPols[indx++] = i*(nz*2-2)*m+j;
}
//inside & outside, number of polygons: (nz-1)*2*(n-1)
for (k = 0; k < (nz-1); k++) {
i = 0;
for (j = 0; j < n-1; j++) {
buff.fPols[indx++] = c+i;
buff.fPols[indx++] = 4;
buff.fPols[indx++] = (2*k+i*1)*m+j;
buff.fPols[indx++] = nz*2*m+(2*k+i*1+2)*n+j;
buff.fPols[indx++] = (2*k+i*1+2)*m+j;
buff.fPols[indx++] = nz*2*m+(2*k+i*1+2)*n+j+1;
}
if (specialCase) {
buff.fPols[indx++] = c+i;
buff.fPols[indx++] = 4;
buff.fPols[indx++] = (2*k+i*1)*m+j;
buff.fPols[indx++] = nz*2*m+(2*k+i*1+2)*n+j;
buff.fPols[indx++] = (2*k+i*1+2)*m+j;
buff.fPols[indx++] = nz*2*m+(2*k+i*1+2)*n;
}
i = 1;
for (j = 0; j < n-1; j++) {
buff.fPols[indx++] = c+i;
buff.fPols[indx++] = 4;
buff.fPols[indx++] = nz*2*m+(2*k+i*1+2)*n+j+1;
buff.fPols[indx++] = (2*k+i*1+2)*m+j;
buff.fPols[indx++] = nz*2*m+(2*k+i*1+2)*n+j;
buff.fPols[indx++] = (2*k+i*1)*m+j;
}
if (specialCase) {
buff.fPols[indx++] = c+i;
buff.fPols[indx++] = 4;
buff.fPols[indx++] = nz*2*m+(2*k+i*1+2)*n;
buff.fPols[indx++] = (2*k+i*1+2)*m+j;
buff.fPols[indx++] = nz*2*m+(2*k+i*1+2)*n+j;
buff.fPols[indx++] = (2*k+i*1)*m+j;
}
}
//left & right sections, number of polygons: 2*(nz-1)
// special case number of polygons: 0
if (!specialCase) {
indx2 = nz*2*(n-1);
for (k = 0; k < (nz-1); k++) {
i = 0;
buff.fPols[indx++] = c+2;
buff.fPols[indx++] = 4;
buff.fPols[indx++] = k==0 ? indx2+i*(n-1) : indx2+2*nz*n+2*(k-1)+i;
buff.fPols[indx++] = indx2+(2*k+3)*n+i*(n-1);
buff.fPols[indx++] = indx2+2*nz*n+2*k+i;
buff.fPols[indx++] = indx2+2*(k+1)*n+i*(n-1);
i = 1;
buff.fPols[indx++] = c+2;
buff.fPols[indx++] = 4;
buff.fPols[indx++] = k==0 ? indx2+i*(n-1) : indx2+2*nz*n+2*(k-1)+i;
buff.fPols[indx++] = indx2+2*(k+1)*n+i*(n-1);
buff.fPols[indx++] = indx2+2*nz*n+2*k+i;
buff.fPols[indx++] = indx2+(2*k+3)*n+i*(n-1);
}
buff.fPols[indx-8] = indx2+n;
buff.fPols[indx-2] = indx2+2*n-1;
}
}
//_____________________________________________________________________________
Double_t TGeoSphere::Safety(Double_t *point, Bool_t in) const
{
// computes the closest distance from given point to this shape, according
// to option. The matching point on the shape is stored in spoint.
Double_t r2 = point[0]*point[0]+point[1]*point[1]+point[2]*point[2];
Double_t r=TMath::Sqrt(r2);
Bool_t rzero=kFALSE;
if (r<=1E-20) rzero=kTRUE;
//localize theta
Double_t th=0.;
if (TestShapeBit(kGeoThetaSeg) && (!rzero)) {
th = TMath::ACos(point[2]/r)*TMath::RadToDeg();
}
Double_t saf[4];
saf[0]=(fRmin==0 && !TestShapeBit(kGeoThetaSeg) && !TestShapeBit(kGeoPhiSeg))?TGeoShape::Big():r-fRmin;
saf[1]=fRmax-r;
saf[2]=saf[3]= TGeoShape::Big();
if (TestShapeBit(kGeoThetaSeg)) {
if (fTheta1>0) saf[2] = r*TMath::Sin((th-fTheta1)*TMath::DegToRad());
if (fTheta2<180) saf[3] = r*TMath::Sin((fTheta2-th)*TMath::DegToRad());
}
Double_t safphi = TGeoShape::Big();
Double_t safe = TGeoShape::Big();
if (TestShapeBit(kGeoPhiSeg)) safphi = TGeoShape::SafetyPhi(point,in,fPhi1,fPhi2);
if (in) {
safe = saf[TMath::LocMin(4,saf)];
return TMath::Min(safe,safphi);
}
for (Int_t i=0; i<4; i++) saf[i]=-saf[i];
safe = saf[TMath::LocMax(4, saf)];
if (TestShapeBit(kGeoPhiSeg)) return TMath::Max(safe, safphi);
return safe;
}
//_____________________________________________________________________________
void TGeoSphere::SavePrimitive(ofstream &out, Option_t * /*option*/)
{
// Save a primitive as a C++ statement(s) on output stream "out".
if (TObject::TestBit(kGeoSavePrimitive)) return;
out << " // Shape: " << GetName() << " type: " << ClassName() << endl;
out << " rmin = " << fRmin << ";" << endl;
out << " rmax = " << fRmax << ";" << endl;
out << " theta1 = " << fTheta1<< ";" << endl;
out << " theta2 = " << fTheta2 << ";" << endl;
out << " phi1 = " << fPhi1 << ";" << endl;
out << " phi2 = " << fPhi2 << ";" << endl;
out << " TGeoShape *" << GetPointerName() << " = new TGeoSphere(\"" << GetName() << "\",rmin,rmax,theta1, theta2,phi1,phi2);" << endl;
TObject::SetBit(TGeoShape::kGeoSavePrimitive);
}
//_____________________________________________________________________________
void TGeoSphere::SetSphDimensions(Double_t rmin, Double_t rmax, Double_t theta1,
Double_t theta2, Double_t phi1, Double_t phi2)
{
if (rmin >= rmax) {
Error("SetDimensions", "invalid parameters rmin/rmax");
return;
}
fRmin = rmin;
fRmax = rmax;
if (rmin>0) SetShapeBit(kGeoRSeg);
if (theta1 >= theta2 || theta1<0 || theta1>180 || theta2>180) {
Error("SetDimensions", "invalid parameters theta1/theta2");
return;
}
fTheta1 = theta1;
fTheta2 = theta2;
if ((theta2-theta1)<180.) SetShapeBit(kGeoThetaSeg);
fPhi1 = phi1;
if (phi1<0) fPhi1+=360.;
fPhi2 = phi2;
while (fPhi2<fPhi1) fPhi2+=360.;
if (TMath::Abs(phi2-phi1)!=360.) SetShapeBit(kGeoPhiSeg);
}
//_____________________________________________________________________________
void TGeoSphere::SetDimensions(Double_t *param)
{
Double_t rmin = param[0];
Double_t rmax = param[1];
Double_t theta1 = 0;
Double_t theta2 = 180.;
Double_t phi1 = 0;
Double_t phi2 = 360.;
// if (nparam > 2) theta1 = param[2];
// if (nparam > 3) theta2 = param[3];
// if (nparam > 4) phi1 = param[4];
// if (nparam > 5) phi2 = param[5];
SetSphDimensions(rmin, rmax, theta1, theta2, phi1, phi2);
}
//_____________________________________________________________________________
void TGeoSphere::SetNumberOfDivisions(Int_t p)
{
fNseg = p;
Double_t dphi = fPhi2 - fPhi1;
if (dphi<0) dphi+=360;
Double_t dtheta = TMath::Abs(fTheta2-fTheta1);
fNz = Int_t(fNseg*dtheta/dphi) +1;
}
//_____________________________________________________________________________
void TGeoSphere::SetPoints(Double_t *points) const
{
// create sphere mesh points
Int_t i,j ;
if (points) {
Double_t dphi = fPhi2-fPhi1;
if (dphi<0) dphi+=360;
Double_t dtheta = fTheta2-fTheta1;
Int_t n = fNseg + 1;
dphi = dphi/fNseg;
dtheta = dtheta/fNz;
Double_t z, theta, phi, cphi, sphi;
Int_t indx=0;
for (i = 0; i < fNz+1; i++)
{
theta = (fTheta1+i*dtheta)*TMath::DegToRad();
z = fRmin * TMath::Cos(theta); // fSinPhiTab[i];
Double_t zi = fRmin*TMath::Sin(theta);
// printf("plane %i nseg=%i z=%f:\n", i,n,z);
for (j = 0; j < n; j++) {
phi = (fPhi1+j*dphi)*TMath::DegToRad();
cphi = TMath::Cos(phi);
sphi = TMath::Sin(phi);
points[indx++] = zi * cphi;
points[indx++] = zi * sphi;
points[indx++] = z;
// printf("%i %f %f %f\n", j, points[3*j], points[3*j+1], points[3*j+2]);
}
z = fRmax * TMath::Cos(theta);
zi = fRmax* TMath::Sin(theta);
// printf("outer points for plane %i:\n", i);
for (j = 0; j < n; j++) {
phi = (fPhi1+j*dphi)*TMath::DegToRad();
cphi = TMath::Cos(phi);
sphi = TMath::Sin(phi);
points[indx++] = zi * cphi;
points[indx++] = zi * sphi;
points[indx++] = z;
// printf("%i %f %f %f\n", j, points[n+3*j], points[n+3*j+1], points[n+3*j+2]);
}
}
}
}
//_____________________________________________________________________________
void TGeoSphere::SetPoints(Float_t *points) const
{
// create sphere mesh points
Int_t i,j ;
if (points) {
Double_t dphi = fPhi2-fPhi1;
if (dphi<0) dphi+=360;
Double_t dtheta = fTheta2-fTheta1;
Int_t n = fNseg + 1;
dphi = dphi/fNseg;
dtheta = dtheta/fNz;
Double_t z, theta, phi, cphi, sphi;
Int_t indx=0;
for (i = 0; i < fNz+1; i++)
{
theta = (fTheta1+i*dtheta)*TMath::DegToRad();
z = fRmin * TMath::Cos(theta); // fSinPhiTab[i];
Double_t zi = fRmin*TMath::Sin(theta);
// printf("plane %i nseg=%i z=%f:\n", i,n,z);
for (j = 0; j < n; j++)
{
phi = (fPhi1+j*dphi)*TMath::DegToRad();
cphi = TMath::Cos(phi);
sphi = TMath::Sin(phi);
points[indx++] = zi * cphi;
points[indx++] = zi * sphi;
points[indx++] = z;
// printf("%i %f %f %f\n", j, points[3*j], points[3*j+1], points[3*j+2]);
}
z = fRmax * TMath::Cos(theta);
zi = fRmax* TMath::Sin(theta);
// printf("outer points for plane %i:\n", i);
for (j = 0; j < n; j++)
{
phi = (fPhi1+j*dphi)*TMath::DegToRad();
cphi = TMath::Cos(phi);
sphi = TMath::Sin(phi);
points[indx++] = zi * cphi;
points[indx++] = zi * sphi;
points[indx++] = z;
// printf("%i %f %f %f\n", j, points[n+3*j], points[n+3*j+1], points[n+3*j+2]);
}
}
}
}
//_____________________________________________________________________________
Int_t TGeoSphere::GetNmeshVertices() const
{
// Return number of vertices of the mesh representation
Int_t n;
n = fNseg+1;
Int_t nz = fNz+1;
Int_t numPoints = 2*n*nz;
return numPoints;
}
//_____________________________________________________________________________
void TGeoSphere::Sizeof3D() const
{
///// fill size of this 3-D object
/// TVirtualGeoPainter *painter = gGeoManager->GetGeomPainter();
/// if (!painter) return;
///
/// Int_t n;
/// n = fNseg+1;
/// Int_t nz = fNz+1;
/// Bool_t specialCase = kFALSE;
///
/// if (TMath::Abs(TMath::Sin(2*(fPhi2 - fPhi1))) <= 0.01) //mark this as a very special case, when
/// specialCase = kTRUE; //we have to draw this PCON like a TUBE
///
/// Int_t numPoints = 2*n*nz;
/// Int_t numSegs = 4*(nz*n-1+(specialCase == kTRUE));
/// Int_t numPolys = 2*(nz*n-1+(specialCase == kTRUE));
/// painter->AddSize3D(numPoints, numSegs, numPolys);
}
const TBuffer3D & TGeoSphere::GetBuffer3D(Int_t reqSections, Bool_t localFrame) const
{
static TBuffer3DSphere buffer;
TGeoBBox::FillBuffer3D(buffer, reqSections, localFrame);
if (reqSections & TBuffer3D::kShapeSpecific) {
buffer.fRadiusInner = fRmin;
buffer.fRadiusOuter = fRmax;
buffer.fThetaMin = fTheta1;
buffer.fThetaMax = fTheta2;
buffer.fPhiMin = fPhi1;
buffer.fPhiMax = fPhi2;
buffer.SetSectionsValid(TBuffer3D::kShapeSpecific);
}
if (reqSections & TBuffer3D::kRawSizes) {
// We want FillBuffer to be const
TGeoSphere * localThis = const_cast<TGeoSphere *>(this);
localThis->SetNumberOfDivisions(gGeoManager->GetNsegments());
Int_t n = GetNumberOfDivisions()+1;
Int_t nz = GetNz()+1;
Int_t NbPnts = 2*n*nz;
if (nz < 2 || NbPnts <= 0) {
assert(kFALSE);
}
else {
Bool_t specialCase = (TMath::Abs(TMath::Sin(2*(fPhi2 - fPhi1))) <= 0.01);
Int_t NbSegs = 4*(nz*n-1+(specialCase == kTRUE));
Int_t NbPols = 2*(nz*n-1+(specialCase == kTRUE));
if (buffer.SetRawSizes(NbPnts, 3*NbPnts, NbSegs, 3*NbSegs, NbPols, 6*NbPols)) {
buffer.SetSectionsValid(TBuffer3D::kRawSizes);
}
}
}
if ((reqSections & TBuffer3D::kRaw) && buffer.SectionsValid(TBuffer3D::kRawSizes)) {
SetPoints(buffer.fPnts);
if (!buffer.fLocalFrame) {
TransformPoints(buffer.fPnts, buffer.NbPnts());
}
SetSegsAndPols(buffer);
buffer.SetSectionsValid(TBuffer3D::kRaw);
}
return buffer;
}
*/
//
#include "Riostream.h"
#include "TROOT.h"
#include "TGeoCone.h"
#include "TGeoManager.h"
#include "TGeoVolume.h"
#include "TVirtualGeoPainter.h"
#include "TGeoSphere.h"
#include "TVirtualPad.h"
#include "TBuffer3D.h"
#include "TBuffer3DTypes.h"
ClassImp(TGeoSphere)
//_____________________________________________________________________________
TGeoSphere::TGeoSphere()
{
// Default constructor
SetShapeBit(TGeoShape::kGeoSph);
fNz = 0;
fNseg = 0;
fRmin = 0.0;
fRmax = 0.0;
fTheta1 = 0.0;
fTheta2 = 180.0;
fPhi1 = 0.0;
fPhi2 = 360.0;
}
//_____________________________________________________________________________
TGeoSphere::TGeoSphere(Double_t rmin, Double_t rmax, Double_t theta1,
Double_t theta2, Double_t phi1, Double_t phi2)
:TGeoBBox(0, 0, 0)
{
// Default constructor specifying minimum and maximum radius
SetShapeBit(TGeoShape::kGeoSph);
SetSphDimensions(rmin, rmax, theta1, theta2, phi1, phi2);
ComputeBBox();
SetNumberOfDivisions(20);
}
//_____________________________________________________________________________
TGeoSphere::TGeoSphere(const char *name, Double_t rmin, Double_t rmax, Double_t theta1,
Double_t theta2, Double_t phi1, Double_t phi2)
:TGeoBBox(name, 0, 0, 0)
{
// Default constructor specifying minimum and maximum radius
SetShapeBit(TGeoShape::kGeoSph);
SetSphDimensions(rmin, rmax, theta1, theta2, phi1, phi2);
ComputeBBox();
SetNumberOfDivisions(20);
}
//_____________________________________________________________________________
TGeoSphere::TGeoSphere(Double_t *param, Int_t /*nparam*/)
:TGeoBBox(0, 0, 0)
{
// Default constructor specifying minimum and maximum radius
// param[0] = Rmin
// param[1] = Rmax
SetShapeBit(TGeoShape::kGeoSph);
SetDimensions(param);
ComputeBBox();
SetNumberOfDivisions(20);
}
//_____________________________________________________________________________
TGeoSphere::~TGeoSphere()
{
// destructor
}
//_____________________________________________________________________________
void TGeoSphere::ComputeBBox()
{
// compute bounding box of the sphere
// Double_t xmin, xmax, ymin, ymax, zmin, zmax;
if (TMath::Abs(fTheta2-fTheta1) == 180) {
if (TMath::Abs(fPhi2-fPhi1) == 360) {
TGeoBBox::SetBoxDimensions(fRmax, fRmax, fRmax);
memset(fOrigin, 0, 3*sizeof(Double_t));
return;
}
}
Double_t st1 = TMath::Sin(fTheta1*TMath::DegToRad());
Double_t st2 = TMath::Sin(fTheta2*TMath::DegToRad());
Double_t r1min, r1max, r2min, r2max, rmin, rmax;
r1min = TMath::Min(fRmax*st1, fRmax*st2);
r1max = TMath::Max(fRmax*st1, fRmax*st2);
r2min = TMath::Min(fRmin*st1, fRmin*st2);
r2max = TMath::Max(fRmin*st1, fRmin*st2);
if (((fTheta1<=90) && (fTheta2>=90)) || ((fTheta2<=90) && (fTheta1>=90))) {
r1max = fRmax;
r2max = fRmin;
}
rmin = TMath::Min(r1min, r2min);
rmax = TMath::Max(r1max, r2max);
Double_t xc[4];
Double_t yc[4];
xc[0] = rmax*TMath::Cos(fPhi1*TMath::DegToRad());
yc[0] = rmax*TMath::Sin(fPhi1*TMath::DegToRad());
xc[1] = rmax*TMath::Cos(fPhi2*TMath::DegToRad());
yc[1] = rmax*TMath::Sin(fPhi2*TMath::DegToRad());
xc[2] = rmin*TMath::Cos(fPhi1*TMath::DegToRad());
yc[2] = rmin*TMath::Sin(fPhi1*TMath::DegToRad());
xc[3] = rmin*TMath::Cos(fPhi2*TMath::DegToRad());
yc[3] = rmin*TMath::Sin(fPhi2*TMath::DegToRad());
Double_t xmin = xc[TMath::LocMin(4, &xc[0])];
Double_t xmax = xc[TMath::LocMax(4, &xc[0])];
Double_t ymin = yc[TMath::LocMin(4, &yc[0])];
Double_t ymax = yc[TMath::LocMax(4, &yc[0])];
Double_t dp = fPhi2-fPhi1;
if (dp<0) dp+=360;
Double_t ddp = -fPhi1;
if (ddp<0) ddp+= 360;
if (ddp>360) ddp-=360;
if (ddp<=dp) xmax = rmax;
ddp = 90-fPhi1;
if (ddp<0) ddp+= 360;
if (ddp>360) ddp-=360;
if (ddp<=dp) ymax = rmax;
ddp = 180-fPhi1;
if (ddp<0) ddp+= 360;
if (ddp>360) ddp-=360;
if (ddp<=dp) xmin = -rmax;
ddp = 270-fPhi1;
if (ddp<0) ddp+= 360;
if (ddp>360) ddp-=360;
if (ddp<=dp) ymin = -rmax;
xc[0] = fRmax*TMath::Cos(fTheta1*TMath::DegToRad());
xc[1] = fRmax*TMath::Cos(fTheta2*TMath::DegToRad());
xc[2] = fRmin*TMath::Cos(fTheta1*TMath::DegToRad());
xc[3] = fRmin*TMath::Cos(fTheta2*TMath::DegToRad());
Double_t zmin = xc[TMath::LocMin(4, &xc[0])];
Double_t zmax = xc[TMath::LocMax(4, &xc[0])];
fOrigin[0] = (xmax+xmin)/2;
fOrigin[1] = (ymax+ymin)/2;
fOrigin[2] = (zmax+zmin)/2;;
fDX = (xmax-xmin)/2;
fDY = (ymax-ymin)/2;
fDZ = (zmax-zmin)/2;
}
//_____________________________________________________________________________
void TGeoSphere::ComputeNormal(Double_t *point, Double_t *dir, Double_t *norm)
{
// Compute normal to closest surface from POINT.
Double_t rxy2 = point[0]*point[0]+point[1]*point[1];
Double_t r2 = rxy2+point[2]*point[2];
Double_t r=TMath::Sqrt(r2);
Bool_t rzero=kFALSE;
if (r<=1E-20) rzero=kTRUE;
//localize theta
Double_t phi=0;
Double_t th=0.;
if (!rzero) th = TMath::ACos(point[2]/r);
//localize phi
phi=TMath::ATan2(point[1], point[0]);
Double_t saf[4];
saf[0]=(fRmin==0 && !TestShapeBit(kGeoThetaSeg) && !TestShapeBit(kGeoPhiSeg))?TGeoShape::Big():TMath::Abs(r-fRmin);
saf[1]=TMath::Abs(fRmax-r);
saf[2]=saf[3]= TGeoShape::Big();
if (TestShapeBit(kGeoThetaSeg)) {
if (fTheta1>0) {
saf[2] = r*TMath::Abs(TMath::Sin(th-fTheta1*TMath::DegToRad()));
}
if (fTheta2<180) {
saf[3] = r*TMath::Abs(TMath::Sin(fTheta2*TMath::DegToRad()-th));
}
}
Int_t i = TMath::LocMin(4,saf);
if (TestShapeBit(kGeoPhiSeg)) {
Double_t c1 = TMath::Cos(fPhi1*TMath::DegToRad());
Double_t s1 = TMath::Sin(fPhi1*TMath::DegToRad());
Double_t c2 = TMath::Cos(fPhi2*TMath::DegToRad());
Double_t s2 = TMath::Sin(fPhi2*TMath::DegToRad());
if (TGeoShape::IsCloseToPhi(saf[i], point,c1,s1,c2,s2)) {
TGeoShape::NormalPhi(point,dir,norm,c1,s1,c2,s2);
return;
}
}
if (i>1) {
if (i==2) th=(fTheta1<90)?(fTheta1+90):(fTheta1-90);
else th=(fTheta2<90)?(fTheta2+90):(fTheta2-90);
th *= TMath::DegToRad();
}
norm[0] = TMath::Sin(th)*TMath::Cos(phi);
norm[1] = TMath::Sin(th)*TMath::Sin(phi);
norm[2] = TMath::Cos(th);
if (norm[0]*dir[0]+norm[1]*dir[1]+norm[2]*dir[2]<0) {
norm[0] = -norm[0];
norm[1] = -norm[1];
norm[2] = -norm[2];
}
}
//_____________________________________________________________________________
Bool_t TGeoSphere::IsPointInside(Double_t *point, Bool_t checkR, Bool_t checkTh, Bool_t checkPh) const
{
Double_t r2 = point[0]*point[0]+point[1]*point[1]+point[2]*point[2];
if (checkR) {
if (TestShapeBit(kGeoRSeg) && (r2<fRmin*fRmin)) return kFALSE;
if (r2>fRmax*fRmax) return kFALSE;
}
if (r2<1E-20) return kTRUE;
if (checkPh && TestShapeBit(kGeoPhiSeg)) {
Double_t phi = TMath::ATan2(point[1], point[0]) * TMath::RadToDeg();
while (phi < fPhi1) phi+=360.;
Double_t dphi = fPhi2 -fPhi1;
Double_t ddp = phi - fPhi1;
if (ddp > dphi) return kFALSE;
}
if (checkTh && TestShapeBit(kGeoThetaSeg)) {
r2=TMath::Sqrt(r2);
// check theta range
Double_t theta = TMath::ACos(point[2]/r2)*TMath::RadToDeg();
if ((theta<fTheta1) || (theta>fTheta2)) return kFALSE;
}
return kTRUE;
}
//_____________________________________________________________________________
Bool_t TGeoSphere::Contains(Double_t *point) const
{
// test if point is inside this sphere
// check Rmin<=R<=Rmax
Double_t r2=point[0]*point[0]+point[1]*point[1]+point[2]*point[2];
if (TestShapeBit(kGeoRSeg) && (r2<fRmin*fRmin)) return kFALSE;
if (r2>fRmax*fRmax) return kFALSE;
if (r2<1E-20) return kTRUE;
// check phi range
if (TestShapeBit(kGeoPhiSeg)) {
Double_t phi = TMath::ATan2(point[1], point[0]) * TMath::RadToDeg();
if (phi < 0 ) phi+=360.;
Double_t dphi = fPhi2 -fPhi1;
if (dphi < 0) dphi+=360.;
Double_t ddp = phi - fPhi1;
if (ddp < 0) ddp += 360.;
if (ddp > dphi) return kFALSE;
}
if (TestShapeBit(kGeoThetaSeg)) {
r2=TMath::Sqrt(r2);
// check theta range
Double_t theta = TMath::ACos(point[2]/r2)*TMath::RadToDeg();
if ((theta<fTheta1) || (theta>fTheta2)) return kFALSE;
}
return kTRUE;
}
//_____________________________________________________________________________
Int_t TGeoSphere::DistancetoPrimitive(Int_t px, Int_t py)
{
// compute closest distance from point px,py to each corner
Int_t n = fNseg+1;
Int_t nz = fNz+1;
const Int_t numPoints = 2*n*nz;
return ShapeDistancetoPrimitive(numPoints, px, py);
}
//_____________________________________________________________________________
Double_t TGeoSphere::DistFromOutside(Double_t *point, Double_t *dir, Int_t iact, Double_t step, Double_t *safe) const
{
// compute distance from outside point to surface of the sphere
Double_t saf[6];
Double_t rxy2 = point[0]*point[0]+point[1]*point[1];
Double_t rxy = TMath::Sqrt(rxy2);
Double_t r2 = rxy2+point[2]*point[2];
Double_t r=TMath::Sqrt(r2);
Bool_t rzero=kFALSE;
Double_t phi=0;;
if (r<1E-20) rzero=kTRUE;
//localize theta
Double_t th=0.;
if (TestShapeBit(kGeoThetaSeg) && (!rzero)) {
th = TMath::ACos(point[2]/r)*TMath::RadToDeg();
}
//localize phi
if (TestShapeBit(kGeoPhiSeg)) {
phi=TMath::ATan2(point[1], point[0])*TMath::RadToDeg();
if (phi<0) phi+=360.;
}
if (iact<3 && safe) {
saf[0]=(r<fRmin)?fRmin-r:TGeoShape::Big();
saf[1]=(r>fRmax)?(r-fRmax):TGeoShape::Big();
saf[2]=saf[3]=saf[4]=saf[5]= TGeoShape::Big();
if (TestShapeBit(kGeoThetaSeg)) {
if (th < fTheta1) {
saf[2] = r*TMath::Sin((fTheta1-th)*TMath::DegToRad());
}
if (th > fTheta2) {
saf[3] = r*TMath::Sin((th-fTheta2)*TMath::DegToRad());
}
}
if (TestShapeBit(kGeoPhiSeg)) {
Double_t dph1=phi-fPhi1;
if (dph1<0) dph1+=360.;
if (dph1<=90.) saf[4]=rxy*TMath::Sin(dph1*TMath::DegToRad());
Double_t dph2=fPhi2-phi;
if (dph2<0) dph2+=360.;
if (dph2>90.) saf[5]=rxy*TMath::Sin(dph2*TMath::DegToRad());
}
*safe = saf[TMath::LocMin(6, &saf[0])];
if (iact==0) return TGeoShape::Big();
if (iact==1 && step<*safe) return TGeoShape::Big();
}
// compute distance to shape
Double_t snxt = TGeoShape::Big();
Double_t rdotn = point[0]*dir[0]+point[1]*dir[1]+point[2]*dir[2];
Bool_t fullsph = (!TestShapeBit(kGeoThetaSeg) && !TestShapeBit(kGeoPhiSeg))?kTRUE:kFALSE;
if (fullsph) {
Bool_t inrmax = kFALSE;
Bool_t inrmin = kFALSE;
if (r<=fRmax+TGeoShape::Tolerance()) inrmax = kTRUE;
if (r>=fRmin-TGeoShape::Tolerance()) inrmin = kTRUE;
if (inrmax && inrmin) {
if ((fRmax-r) < (r-fRmin)) {
// close to Rmax
if (rdotn>=0) return TGeoShape::Big();
return 0.0; // already in
}
// close to Rmin
if (fRmin==0.0 || rdotn>=0) return 0.0;
// check second crossing of Rmin
return DistToSphere(point, dir, fRmin, kFALSE, kFALSE);
}
}
// first check if any crossing at all
if (r>fRmax) {
Double_t b = rdotn;
Double_t c = r2-fRmax*fRmax;
Double_t d=b*b-c;
if (d<0) return TGeoShape::Big();
}
// do rmin, rmax, checking phi and theta ranges
if (r<fRmin) {
// check first cross of rmin
snxt = DistToSphere(point, dir, fRmin, kTRUE);
if (snxt<1E20) return snxt;
} else {
if (r>fRmax) {
// point outside rmax, check first cross of rmax
snxt = DistToSphere(point, dir, fRmax, kTRUE);
if (snxt<1E20) return snxt;
// now check first crossing of rmin
if (fRmin>0) {
snxt = DistToSphere(point, dir, fRmin, kTRUE);
// if this is outside range, check second crossing of rmin
if (snxt>1E20) {
snxt = DistToSphere(point, dir, fRmin, kTRUE, kFALSE);
if (snxt<1E20) return snxt;
}
}
} else {
// point between rmin and rmax, check first cross of rmin
snxt = DistToSphere(point, dir, fRmin, kTRUE);
// if this is outside range, check second crossing of rmin
if (snxt>1E20) {
snxt = DistToSphere(point, dir, fRmin, kTRUE, kFALSE);
if (snxt<1E20) return snxt;
}
}
}
// check theta conical surfaces
Double_t ptnew[3];
Double_t b,delta, znew;
Double_t st1=TGeoShape::Big(), st2=TGeoShape::Big();
if (TestShapeBit(kGeoThetaSeg)) {
if (fTheta1>0) {
if (fTheta1==90) {
// surface is a plane
if (point[2]*dir[2]<0) {
snxt = -point[2]/dir[2];
ptnew[0] = point[0]+snxt*dir[0];
ptnew[1] = point[1]+snxt*dir[1];
ptnew[2] = 0;
// check range
if (IsPointInside(&ptnew[0], kTRUE, kFALSE, kTRUE)) return snxt;
}
} else {
Double_t r1,r2,z1,z2,dz;
Double_t si = TMath::Sin(fTheta1*TMath::DegToRad());
Double_t ci = TMath::Cos(fTheta1*TMath::DegToRad());
if (ci>0) {
r1 = fRmin*si;
z1 = fRmin*ci;
r2 = fRmax*si;
z2 = fRmax*ci;
} else {
r1 = fRmax*si;
z1 = fRmax*ci;
r2 = fRmin*si;
z2 = fRmin*ci;
}
dz = 0.5*(z2-z1);
ptnew[0] = point[0];
ptnew[1] = point[1];
ptnew[2] = point[2]-0.5*(z1+z2);
if (TestShapeBit(kGeoPhiSeg)) {
st1 = TGeoConeSeg::DistToCons(point, dir, r1, z1, r2, z2, fPhi1, fPhi2);
} else {
TGeoCone::DistToCone(ptnew, dir, dz, r1, r2, b, delta);
if (delta>0) {
st1 = -b-delta;
znew = ptnew[2]+st1*dir[2];
if (st1<0 || TMath::Abs(znew)>0) {
st1 = -b+delta;
znew = ptnew[2]+st1*dir[2];
if (st1<0 || TMath::Abs(znew)>0) st1=TGeoShape::Big();
}
}
}
}
}
if (fTheta2<180) {
if (fTheta2==90) {
// surface is a plane
if (point[2]*dir[2]<0) {
snxt = -point[2]/dir[2];
ptnew[0] = point[0]+snxt*dir[0];
ptnew[1] = point[1]+snxt*dir[1];
ptnew[2] = 0;
// check range
if (IsPointInside(&ptnew[0], kTRUE, kFALSE, kTRUE)) return snxt;
}
} else {
Double_t r1,r2,z1,z2,dz;
Double_t si = TMath::Sin(fTheta2*TMath::DegToRad());
Double_t ci = TMath::Cos(fTheta2*TMath::DegToRad());
if (ci>0) {
r1 = fRmin*si;
z1 = fRmin*ci;
r2 = fRmax*si;
z2 = fRmax*ci;
} else {
r1 = fRmax*si;
z1 = fRmax*ci;
r2 = fRmin*si;
z2 = fRmin*ci;
}
dz = 0.5*(z2-z1);
ptnew[0] = point[0];
ptnew[1] = point[1];
ptnew[2] = point[2]-0.5*(z1+z2);
if (TestShapeBit(kGeoPhiSeg)) {
st2 = TGeoConeSeg::DistToCons(point, dir, r1, z1, r2, z2, fPhi1, fPhi2);
} else {
TGeoCone::DistToCone(ptnew, dir, dz, r1, r2, b, delta);
if (delta>0) {
st2 = -b-delta;
znew = ptnew[2]+st2*dir[2];
if (st2<0 || TMath::Abs(znew)>dz) {
st2 = -b+delta;
znew = ptnew[2]+st2*dir[2];
if (st2<0 || TMath::Abs(znew)>0) st2=TGeoShape::Big();
}
}
}
}
}
}
snxt = TMath::Min(st1, st2);
// if (snxt<1E20) return snxt;
if (TestShapeBit(kGeoPhiSeg)) {
Double_t s1 = TMath::Sin(fPhi1*TMath::DegToRad());
Double_t c1 = TMath::Cos(fPhi1*TMath::DegToRad());
Double_t s2 = TMath::Sin(fPhi2*TMath::DegToRad());
Double_t c2 = TMath::Cos(fPhi2*TMath::DegToRad());
Double_t phim = 0.5*(fPhi1+fPhi2);
Double_t sm = TMath::Sin(phim*TMath::DegToRad());
Double_t cm = TMath::Cos(phim*TMath::DegToRad());
Double_t sfi1=TGeoShape::Big();
Double_t sfi2=TGeoShape::Big();
Double_t s=0;
Double_t safety, un;
safety = point[0]*s1-point[1]*c1;
if (safety>0) {
un = dir[0]*s1-dir[1]*c1;
if (un<0) {
s=-safety/un;
ptnew[0] = point[0]+s*dir[0];
ptnew[1] = point[1]+s*dir[1];
ptnew[2] = point[2]+s*dir[2];
if ((ptnew[1]*cm-ptnew[0]*sm)<=0) {
sfi1=s;
if (IsPointInside(&ptnew[0], kTRUE, kTRUE, kFALSE) && sfi1<snxt) return sfi1;
}
}
}
safety = -point[0]*s2+point[1]*c2;
if (safety>0) {
un = -dir[0]*s2+dir[1]*c2;
if (un<0) {
s=-safety/un;
ptnew[0] = point[0]+s*dir[0];
ptnew[1] = point[1]+s*dir[1];
ptnew[2] = point[2]+s*dir[2];
if ((ptnew[1]*cm-ptnew[0]*sm)>=0) {
sfi2=s;
if (IsPointInside(&ptnew[0], kTRUE, kTRUE, kFALSE) && sfi2<snxt) return sfi2;
}
}
}
}
return snxt;
}
//_____________________________________________________________________________
Double_t TGeoSphere::DistFromInside(Double_t *point, Double_t *dir, Int_t iact, Double_t step, Double_t *safe) const
{
// compute distance from inside point to surface of the sphere
Double_t saf[6];
Double_t rxy2 = point[0]*point[0]+point[1]*point[1];
Double_t rxy = TMath::Sqrt(rxy2);
Double_t r2 = rxy2+point[2]*point[2];
Double_t r=TMath::Sqrt(r2);
Bool_t rzero=kFALSE;
if (r<=1E-20) rzero=kTRUE;
//localize theta
Double_t phi=0;;
Double_t th=0.;
if (TestShapeBit(kGeoThetaSeg) && (!rzero)) {
th = TMath::ACos(point[2]/r)*TMath::RadToDeg();
}
//localize phi
if (TestShapeBit(kGeoPhiSeg)) {
phi=TMath::ATan2(point[1], point[0])*TMath::RadToDeg();
if (phi<0) phi+=360.;
}
if (iact<3 && safe) {
saf[0]=(fRmin==0)?TGeoShape::Big():r-fRmin;
saf[1]=fRmax-r;
saf[2]=saf[3]=saf[4]=saf[5]= TGeoShape::Big();
if (TestShapeBit(kGeoThetaSeg)) {
if (fTheta1>0) {
saf[2] = r*TMath::Sin((th-fTheta1)*TMath::DegToRad());
}
if (fTheta2<180) {
saf[3] = r*TMath::Sin((fTheta2-th)*TMath::DegToRad());
}
}
if (TestShapeBit(kGeoPhiSeg)) {
Double_t dph1=phi-fPhi1;
if (dph1<0) dph1+=360.;
if (dph1<=90.) saf[4]=rxy*TMath::Sin(dph1*TMath::DegToRad());
Double_t dph2=fPhi2-phi;
if (dph2<0) dph2+=360.;
if (dph2<=90.) saf[5]=rxy*TMath::Sin(dph2*TMath::DegToRad());
}
*safe = saf[TMath::LocMin(6, &saf[0])];
if (iact==0) return TGeoShape::Big();
if (iact==1 && step<*safe) return TGeoShape::Big();
}
// compute distance to shape
Double_t snxt = TGeoShape::Big();
if (rzero) {
// gGeoManager->SetNormalChecked(1.);
return fRmax;
}
// first do rmin, rmax
Double_t b,delta, znew;
Double_t rdotn = point[0]*dir[0]+point[1]*dir[1]+point[2]*dir[2];
Double_t sn1 = TGeoShape::Big();
// Inner sphere
if (fRmin>0) {
// Protection in case point is actually outside the sphere
if (r <= fRmin+TGeoShape::Tolerance()) {
if (rdotn<0) return 0.0;
} else {
if (rdotn<0) sn1 = DistToSphere(point, dir, fRmin, kFALSE);
}
}
Double_t sn2 = TGeoShape::Big();
// Outer sphere
if (r >= fRmax-TGeoShape::Tolerance()) {
if (rdotn>=0) return 0.0;
}
sn2 = DistToSphere(point, dir, fRmax, kFALSE);
Double_t sr = TMath::Min(sn1, sn2);
// check theta conical surfaces
sn1 = TGeoShape::Big();
sn2 = TGeoShape::Big();
if (TestShapeBit(kGeoThetaSeg)) {
if (fTheta1==90) {
// surface is a plane
if (point[2]*dir[2]<0) sn1 = -point[2]/dir[2];
} else {
if (fTheta1>0) {
Double_t r1,r2,z1,z2,dz,ptnew[3];
Double_t si = TMath::Sin(fTheta1*TMath::DegToRad());
Double_t ci = TMath::Cos(fTheta1*TMath::DegToRad());
if (ci>0) {
r1 = fRmin*si;
z1 = fRmin*ci;
r2 = fRmax*si;
z2 = fRmax*ci;
} else {
r1 = fRmax*si;
z1 = fRmax*ci;
r2 = fRmin*si;
z2 = fRmin*ci;
}
dz = 0.5*(z2-z1);
ptnew[0] = point[0];
ptnew[1] = point[1];
ptnew[2] = point[2]-0.5*(z1+z2);
if (TestShapeBit(kGeoPhiSeg)) {
sn1 = TGeoConeSeg::DistToCons(point, dir, r1, z1, r2, z2, fPhi1, fPhi2);
} else {
TGeoCone::DistToCone(ptnew, dir, dz, r1, r2, b, delta);
if (delta>0) {
sn1 = -b-delta;
znew = ptnew[2]+sn1*dir[2];
if (sn1<0 || TMath::Abs(znew)>dz) {
sn1 = -b+delta;
znew = ptnew[2]+sn1*dir[2];
if (sn1<0 || TMath::Abs(znew)>0) sn1=TGeoShape::Big();
}
}
}
}
}
if (fTheta2==90) {
// surface is a plane
if (point[2]*dir[2]<0) sn1 = -point[2]/dir[2];
} else {
if (fTheta2<180) {
Double_t r1,r2,z1,z2,dz,ptnew[3];
Double_t si = TMath::Sin(fTheta2*TMath::DegToRad());
Double_t ci = TMath::Cos(fTheta2*TMath::DegToRad());
if (ci>0) {
r1 = fRmin*si;
z1 = fRmin*ci;
r2 = fRmax*si;
z2 = fRmax*ci;
} else {
r1 = fRmax*si;
z1 = fRmax*ci;
r2 = fRmin*si;
z2 = fRmin*ci;
}
dz = 0.5*(z2-z1);
ptnew[0] = point[0];
ptnew[1] = point[1];
ptnew[2] = point[2]-0.5*(z1+z2);
if (TestShapeBit(kGeoPhiSeg)) {
sn2 = TGeoConeSeg::DistToCons(point, dir, r1, z1, r2, z2, fPhi1, fPhi2);
} else {
TGeoCone::DistToCone(ptnew, dir, dz, r1, r2, b, delta);
if (delta>0) {
sn2 = -b-delta;
znew = ptnew[2]+sn2*dir[2];
if (sn2<0 || TMath::Abs(znew)>0) {
sn2 = -b+delta;
znew = ptnew[2]+sn2*dir[2];
if (sn2<0 || TMath::Abs(znew)>0) sn2=TGeoShape::Big();
}
}
}
}
}
}
Double_t st = TMath::Min(sn1,sn2);
Double_t sp = TGeoShape::Big();
if (TestShapeBit(kGeoPhiSeg)) {
Double_t s1 = TMath::Sin(fPhi1*TMath::DegToRad());
Double_t c1 = TMath::Cos(fPhi1*TMath::DegToRad());
Double_t s2 = TMath::Sin(fPhi2*TMath::DegToRad());
Double_t c2 = TMath::Cos(fPhi2*TMath::DegToRad());
Double_t phim = 0.5*(fPhi1+fPhi2);
Double_t sm = TMath::Sin(phim*TMath::DegToRad());
Double_t cm = TMath::Cos(phim*TMath::DegToRad());
sp = TGeoShape::DistToPhiMin(point, dir, s1, c1, s2, c2, sm, cm);
}
snxt = TMath::Min(sr, st);
snxt = TMath::Min(snxt, sp);
return snxt;
}
//_____________________________________________________________________________
Double_t TGeoSphere::DistToSphere(Double_t *point, Double_t *dir, Double_t rsph, Bool_t check, Bool_t firstcross) const
{
// compute distance to sphere of radius rsph. Direction has to be a unit vector
if (rsph<=0) return TGeoShape::Big();
Double_t s=TGeoShape::Big();
Double_t r2 = point[0]*point[0]+point[1]*point[1]+point[2]*point[2];
Double_t b = point[0]*dir[0]+point[1]*dir[1]+point[2]*dir[2];
Double_t c = r2-rsph*rsph;
Bool_t in = (c<=0)?kTRUE:kFALSE;
Double_t d;
d=b*b-c;
if (d<0) return TGeoShape::Big();
Double_t pt[3];
Int_t i;
d = TMath::Sqrt(d);
if (in) {
s=-b+d;
} else {
s = (firstcross)?(-b-d):(-b+d);
}
if (s<0) return TGeoShape::Big();
if (!check) return s;
for (i=0; i<3; i++) pt[i]=point[i]+s*dir[i];
// check theta and phi ranges
if (IsPointInside(&pt[0], kFALSE)) return s;
return TGeoShape::Big();
}
//_____________________________________________________________________________
TGeoVolume *TGeoSphere::Divide(TGeoVolume * /*voldiv*/, const char * /*divname*/, Int_t /*iaxis*/, Int_t /*ndiv*/,
Double_t /*start*/, Double_t /*step*/)
{
// Divide all range of iaxis in range/step cells
Error("Divide", "Division of a sphere not implemented");
return 0;
}
//_____________________________________________________________________________
const char *TGeoSphere::GetAxisName(Int_t iaxis) const
{
// Returns name of axis IAXIS.
switch (iaxis) {
case 1:
return "R";
case 2:
return "THETA";
case 3:
return "PHI";
default:
return "UNDEFINED";
}
}
//_____________________________________________________________________________
Double_t TGeoSphere::GetAxisRange(Int_t iaxis, Double_t &xlo, Double_t &xhi) const
{
// Get range of shape for a given axis.
xlo = 0;
xhi = 0;
Double_t dx = 0;
switch (iaxis) {
case 1:
xlo = fRmin;
xhi = fRmax;
dx = xhi-xlo;
return dx;
case 2:
xlo = fPhi1;
xhi = fPhi2;
dx = xhi-xlo;
return dx;
case 3:
xlo = fTheta1;
xhi = fTheta2;
dx = xhi-xlo;
return dx;
}
return dx;
}
//_____________________________________________________________________________
void TGeoSphere::GetBoundingCylinder(Double_t *param) const
{
//--- Fill vector param[4] with the bounding cylinder parameters. The order
// is the following : Rmin, Rmax, Phi1, Phi2
Double_t smin = TMath::Sin(fTheta1*TMath::DegToRad());
Double_t smax = TMath::Sin(fTheta2*TMath::DegToRad());
if (smin>smax) {
Double_t a = smin;
smin = smax;
smax = a;
}
param[0] = fRmin*smin; // Rmin
param[0] *= param[0];
if (((90.-fTheta1)*(fTheta2-90.))>=0) smax = 1.;
param[1] = fRmax*smax; // Rmax
param[1] *= param[1];
param[2] = (fPhi1<0)?(fPhi1+360.):fPhi1; // Phi1
param[3] = fPhi2;
if ((param[3]-param[2])==360.) { // Phi2
param[2] = 0.;
param[3] = 360.;
}
while (param[3]<param[2]) param[3]+=360.;
}
//_____________________________________________________________________________
void TGeoSphere::InspectShape() const
{
// print shape parameters
printf("*** Shape %s: TGeoSphere ***\n", GetName());
printf(" Rmin = %11.5f\n", fRmin);
printf(" Rmax = %11.5f\n", fRmax);
printf(" Th1 = %11.5f\n", fTheta1);
printf(" Th2 = %11.5f\n", fTheta2);
printf(" Ph1 = %11.5f\n", fPhi1);
printf(" Ph2 = %11.5f\n", fPhi2);
printf(" Bounding box:\n");
TGeoBBox::InspectShape();
}
//_____________________________________________________________________________
TBuffer3D *TGeoSphere::MakeBuffer3D() const
{
// Creates a TBuffer3D describing *this* shape.
// Coordinates are in local reference frame.
Int_t n = gGeoManager->GetNsegments()+1;
Double_t ph1 = GetPhi1();
Double_t ph2 = GetPhi2();
Int_t nz = GetNz()+1;
if (nz < 2) return 0;
Int_t NbPnts = 2*n*nz;
if (NbPnts <= 0) return 0;
Bool_t specialCase = kFALSE;
if (TMath::Abs(TMath::Sin(2*(ph2 - ph1))) <= 0.01) specialCase = kTRUE;
Int_t NbSegs = 4*(nz*n-1+(specialCase == kTRUE));
Int_t NbPols = 2*(nz*n-1+(specialCase == kTRUE));
TBuffer3D* buff = new TBuffer3D(TBuffer3DTypes::kGeneric,
NbPnts, 3*NbPnts, NbSegs, 3*NbSegs, NbPols, 6*NbPols);
if (buff)
{
SetPoints(buff->fPnts);
SetSegsAndPols(*buff);
}
return buff;
}
//_____________________________________________________________________________
void TGeoSphere::SetSegsAndPols(TBuffer3D & buff) const
{
// Fill TBuffer3D structure for segments and polygons.
Int_t i, j;
Int_t n = gGeoManager->GetNsegments()+1;
Double_t ph1 = GetPhi1();
Double_t ph2 = GetPhi2();
Int_t nz = GetNz()+1;
if (nz < 2) return;
Bool_t specialCase = kFALSE;
if (TMath::Abs(TMath::Sin(2*(ph2 - ph1))) <= 0.01) specialCase = kTRUE;
Int_t c = GetBasicColor();
Int_t indx, indx2, k;
indx = indx2 = 0;
//inside & outside spheres, number of segments: 2*nz*(n-1)
// special case number of segments: 2*nz*n
for (i = 0; i < nz*2; i++) {
indx2 = i*n;
for (j = 1; j < n; j++) {
buff.fSegs[indx++] = c;
buff.fSegs[indx++] = indx2+j-1;
buff.fSegs[indx++] = indx2+j;
}
if (specialCase) {
buff.fSegs[indx++] = c;
buff.fSegs[indx++] = indx2+j-1;
buff.fSegs[indx++] = indx2;
}
}
//bottom & top lines, number of segments: 2*n
for (i = 0; i < 2; i++) {
indx2 = i*(nz-1)*2*n;
for (j = 0; j < n; j++) {
buff.fSegs[indx++] = c;
buff.fSegs[indx++] = indx2+j;
buff.fSegs[indx++] = indx2+n+j;
}
}
//inside & outside spheres, number of segments: 2*(nz-1)*n
for (i = 0; i < (nz-1); i++) {
//inside sphere
indx2 = i*n*2;
for (j = 0; j < n; j++) {
buff.fSegs[indx++] = c+2;
buff.fSegs[indx++] = indx2+j;
buff.fSegs[indx++] = indx2+n*2+j;
}
//outside sphere
indx2 = i*n*2+n;
for (j = 0; j < n; j++) {
buff.fSegs[indx++] = c+3;
buff.fSegs[indx++] = indx2+j;
buff.fSegs[indx++] = indx2+n*2+j;
}
}
//left & right sections, number of segments: 2*(nz-2)
// special case number of segments: 0
if (!specialCase) {
for (i = 1; i < (nz-1); i++) {
for (j = 0; j < 2; j++) {
buff.fSegs[indx++] = c;
buff.fSegs[indx++] = 2*i * n + j*(n-1);
buff.fSegs[indx++] = (2*i+1) * n + j*(n-1);
}
}
}
Int_t m = n - 1 + (specialCase == kTRUE);
indx = 0;
//bottom & top, number of polygons: 2*(n-1)
// special case number of polygons: 2*n
i = 0;
for (j = 0; j < n-1; j++) {
buff.fPols[indx++] = c+3;
buff.fPols[indx++] = 4;
buff.fPols[indx++] = i*(nz*2-2)*m+j;
buff.fPols[indx++] = 2*nz*m+i*n+j+1;
buff.fPols[indx++] = i*(nz*2-2)*m+m+j;
buff.fPols[indx++] = 2*nz*m+i*n+j;
}
if (specialCase) {
buff.fPols[indx++] = c+3;
buff.fPols[indx++] = 4;
buff.fPols[indx++] = i*(nz*2-2)*m+j;
buff.fPols[indx++] = 2*nz*m+i*n;
buff.fPols[indx++] = i*(nz*2-2)*m+m+j;
buff.fPols[indx++] = 2*nz*m+i*n+j;
}
i = 1;
for (j = 0; j < n-1; j++) {
buff.fPols[indx++] = c+3;
buff.fPols[indx++] = 4;
buff.fPols[indx++] = 2*nz*m+i*n+j;
buff.fPols[indx++] = i*(nz*2-2)*m+m+j;
buff.fPols[indx++] = 2*nz*m+i*n+j+1;
buff.fPols[indx++] = i*(nz*2-2)*m+j;
}
if (specialCase) {
buff.fPols[indx++] = c+3;
buff.fPols[indx++] = 4;
buff.fPols[indx++] = 2*nz*m+i*n+j;
buff.fPols[indx++] = i*(nz*2-2)*m+m+j;
buff.fPols[indx++] = 2*nz*m+i*n;
buff.fPols[indx++] = i*(nz*2-2)*m+j;
}
//inside & outside, number of polygons: (nz-1)*2*(n-1)
for (k = 0; k < (nz-1); k++) {
i = 0;
for (j = 0; j < n-1; j++) {
buff.fPols[indx++] = c+i;
buff.fPols[indx++] = 4;
buff.fPols[indx++] = (2*k+i*1)*m+j;
buff.fPols[indx++] = nz*2*m+(2*k+i*1+2)*n+j;
buff.fPols[indx++] = (2*k+i*1+2)*m+j;
buff.fPols[indx++] = nz*2*m+(2*k+i*1+2)*n+j+1;
}
if (specialCase) {
buff.fPols[indx++] = c+i;
buff.fPols[indx++] = 4;
buff.fPols[indx++] = (2*k+i*1)*m+j;
buff.fPols[indx++] = nz*2*m+(2*k+i*1+2)*n+j;
buff.fPols[indx++] = (2*k+i*1+2)*m+j;
buff.fPols[indx++] = nz*2*m+(2*k+i*1+2)*n;
}
i = 1;
for (j = 0; j < n-1; j++) {
buff.fPols[indx++] = c+i;
buff.fPols[indx++] = 4;
buff.fPols[indx++] = nz*2*m+(2*k+i*1+2)*n+j+1;
buff.fPols[indx++] = (2*k+i*1+2)*m+j;
buff.fPols[indx++] = nz*2*m+(2*k+i*1+2)*n+j;
buff.fPols[indx++] = (2*k+i*1)*m+j;
}
if (specialCase) {
buff.fPols[indx++] = c+i;
buff.fPols[indx++] = 4;
buff.fPols[indx++] = nz*2*m+(2*k+i*1+2)*n;
buff.fPols[indx++] = (2*k+i*1+2)*m+j;
buff.fPols[indx++] = nz*2*m+(2*k+i*1+2)*n+j;
buff.fPols[indx++] = (2*k+i*1)*m+j;
}
}
//left & right sections, number of polygons: 2*(nz-1)
// special case number of polygons: 0
if (!specialCase) {
indx2 = nz*2*(n-1);
for (k = 0; k < (nz-1); k++) {
i = 0;
buff.fPols[indx++] = c+2;
buff.fPols[indx++] = 4;
buff.fPols[indx++] = k==0 ? indx2+i*(n-1) : indx2+2*nz*n+2*(k-1)+i;
buff.fPols[indx++] = indx2+(2*k+3)*n+i*(n-1);
buff.fPols[indx++] = indx2+2*nz*n+2*k+i;
buff.fPols[indx++] = indx2+2*(k+1)*n+i*(n-1);
i = 1;
buff.fPols[indx++] = c+2;
buff.fPols[indx++] = 4;
buff.fPols[indx++] = k==0 ? indx2+i*(n-1) : indx2+2*nz*n+2*(k-1)+i;
buff.fPols[indx++] = indx2+2*(k+1)*n+i*(n-1);
buff.fPols[indx++] = indx2+2*nz*n+2*k+i;
buff.fPols[indx++] = indx2+(2*k+3)*n+i*(n-1);
}
buff.fPols[indx-8] = indx2+n;
buff.fPols[indx-2] = indx2+2*n-1;
}
}
//_____________________________________________________________________________
Double_t TGeoSphere::Safety(Double_t *point, Bool_t in) const
{
// computes the closest distance from given point to this shape, according
// to option. The matching point on the shape is stored in spoint.
Double_t r2 = point[0]*point[0]+point[1]*point[1]+point[2]*point[2];
Double_t r=TMath::Sqrt(r2);
Bool_t rzero=kFALSE;
if (r<=1E-20) rzero=kTRUE;
//localize theta
Double_t th=0.;
if (TestShapeBit(kGeoThetaSeg) && (!rzero)) {
th = TMath::ACos(point[2]/r)*TMath::RadToDeg();
}
Double_t saf[4];
saf[0]=(fRmin==0 && !TestShapeBit(kGeoThetaSeg) && !TestShapeBit(kGeoPhiSeg))?TGeoShape::Big():r-fRmin;
saf[1]=fRmax-r;
saf[2]=saf[3]= TGeoShape::Big();
if (TestShapeBit(kGeoThetaSeg)) {
if (fTheta1>0) saf[2] = r*TMath::Sin((th-fTheta1)*TMath::DegToRad());
if (fTheta2<180) saf[3] = r*TMath::Sin((fTheta2-th)*TMath::DegToRad());
}
Double_t safphi = TGeoShape::Big();
Double_t safe = TGeoShape::Big();
if (TestShapeBit(kGeoPhiSeg)) safphi = TGeoShape::SafetyPhi(point,in,fPhi1,fPhi2);
if (in) {
safe = saf[TMath::LocMin(4,saf)];
return TMath::Min(safe,safphi);
}
for (Int_t i=0; i<4; i++) saf[i]=-saf[i];
safe = saf[TMath::LocMax(4, saf)];
if (TestShapeBit(kGeoPhiSeg)) return TMath::Max(safe, safphi);
return safe;
}
//_____________________________________________________________________________
void TGeoSphere::SavePrimitive(ofstream &out, Option_t * /*option*/)
{
// Save a primitive as a C++ statement(s) on output stream "out".
if (TObject::TestBit(kGeoSavePrimitive)) return;
out << " // Shape: " << GetName() << " type: " << ClassName() << endl;
out << " rmin = " << fRmin << ";" << endl;
out << " rmax = " << fRmax << ";" << endl;
out << " theta1 = " << fTheta1<< ";" << endl;
out << " theta2 = " << fTheta2 << ";" << endl;
out << " phi1 = " << fPhi1 << ";" << endl;
out << " phi2 = " << fPhi2 << ";" << endl;
out << " TGeoShape *" << GetPointerName() << " = new TGeoSphere(\"" << GetName() << "\",rmin,rmax,theta1, theta2,phi1,phi2);" << endl;
TObject::SetBit(TGeoShape::kGeoSavePrimitive);
}
//_____________________________________________________________________________
void TGeoSphere::SetSphDimensions(Double_t rmin, Double_t rmax, Double_t theta1,
Double_t theta2, Double_t phi1, Double_t phi2)
{
if (rmin >= rmax) {
Error("SetDimensions", "invalid parameters rmin/rmax");
return;
}
fRmin = rmin;
fRmax = rmax;
if (rmin>0) SetShapeBit(kGeoRSeg);
if (theta1 >= theta2 || theta1<0 || theta1>180 || theta2>180) {
Error("SetDimensions", "invalid parameters theta1/theta2");
return;
}
fTheta1 = theta1;
fTheta2 = theta2;
if ((theta2-theta1)<180.) SetShapeBit(kGeoThetaSeg);
fPhi1 = phi1;
if (phi1<0) fPhi1+=360.;
fPhi2 = phi2;
while (fPhi2<fPhi1) fPhi2+=360.;
if (TMath::Abs(phi2-phi1)!=360.) SetShapeBit(kGeoPhiSeg);
}
//_____________________________________________________________________________
void TGeoSphere::SetDimensions(Double_t *param)
{
Double_t rmin = param[0];
Double_t rmax = param[1];
Double_t theta1 = 0;
Double_t theta2 = 180.;
Double_t phi1 = 0;
Double_t phi2 = 360.;
// if (nparam > 2) theta1 = param[2];
// if (nparam > 3) theta2 = param[3];
// if (nparam > 4) phi1 = param[4];
// if (nparam > 5) phi2 = param[5];
SetSphDimensions(rmin, rmax, theta1, theta2, phi1, phi2);
}
//_____________________________________________________________________________
void TGeoSphere::SetNumberOfDivisions(Int_t p)
{
fNseg = p;
Double_t dphi = fPhi2 - fPhi1;
if (dphi<0) dphi+=360;
Double_t dtheta = TMath::Abs(fTheta2-fTheta1);
fNz = Int_t(fNseg*dtheta/dphi) +1;
}
//_____________________________________________________________________________
void TGeoSphere::SetPoints(Double_t *points) const
{
// create sphere mesh points
Int_t i,j ;
if (points) {
Double_t dphi = fPhi2-fPhi1;
if (dphi<0) dphi+=360;
Double_t dtheta = fTheta2-fTheta1;
Int_t n = fNseg + 1;
dphi = dphi/fNseg;
dtheta = dtheta/fNz;
Double_t z, theta, phi, cphi, sphi;
Int_t indx=0;
for (i = 0; i < fNz+1; i++)
{
theta = (fTheta1+i*dtheta)*TMath::DegToRad();
z = fRmin * TMath::Cos(theta); // fSinPhiTab[i];
Double_t zi = fRmin*TMath::Sin(theta);
// printf("plane %i nseg=%i z=%f:\n", i,n,z);
for (j = 0; j < n; j++) {
phi = (fPhi1+j*dphi)*TMath::DegToRad();
cphi = TMath::Cos(phi);
sphi = TMath::Sin(phi);
points[indx++] = zi * cphi;
points[indx++] = zi * sphi;
points[indx++] = z;
// printf("%i %f %f %f\n", j, points[3*j], points[3*j+1], points[3*j+2]);
}
z = fRmax * TMath::Cos(theta);
zi = fRmax* TMath::Sin(theta);
// printf("outer points for plane %i:\n", i);
for (j = 0; j < n; j++) {
phi = (fPhi1+j*dphi)*TMath::DegToRad();
cphi = TMath::Cos(phi);
sphi = TMath::Sin(phi);
points[indx++] = zi * cphi;
points[indx++] = zi * sphi;
points[indx++] = z;
// printf("%i %f %f %f\n", j, points[n+3*j], points[n+3*j+1], points[n+3*j+2]);
}
}
}
}
//_____________________________________________________________________________
void TGeoSphere::SetPoints(Float_t *points) const
{
// create sphere mesh points
Int_t i,j ;
if (points) {
Double_t dphi = fPhi2-fPhi1;
if (dphi<0) dphi+=360;
Double_t dtheta = fTheta2-fTheta1;
Int_t n = fNseg + 1;
dphi = dphi/fNseg;
dtheta = dtheta/fNz;
Double_t z, theta, phi, cphi, sphi;
Int_t indx=0;
for (i = 0; i < fNz+1; i++)
{
theta = (fTheta1+i*dtheta)*TMath::DegToRad();
z = fRmin * TMath::Cos(theta); // fSinPhiTab[i];
Double_t zi = fRmin*TMath::Sin(theta);
// printf("plane %i nseg=%i z=%f:\n", i,n,z);
for (j = 0; j < n; j++)
{
phi = (fPhi1+j*dphi)*TMath::DegToRad();
cphi = TMath::Cos(phi);
sphi = TMath::Sin(phi);
points[indx++] = zi * cphi;
points[indx++] = zi * sphi;
points[indx++] = z;
// printf("%i %f %f %f\n", j, points[3*j], points[3*j+1], points[3*j+2]);
}
z = fRmax * TMath::Cos(theta);
zi = fRmax* TMath::Sin(theta);
// printf("outer points for plane %i:\n", i);
for (j = 0; j < n; j++)
{
phi = (fPhi1+j*dphi)*TMath::DegToRad();
cphi = TMath::Cos(phi);
sphi = TMath::Sin(phi);
points[indx++] = zi * cphi;
points[indx++] = zi * sphi;
points[indx++] = z;
// printf("%i %f %f %f\n", j, points[n+3*j], points[n+3*j+1], points[n+3*j+2]);
}
}
}
}
//_____________________________________________________________________________
Int_t TGeoSphere::GetNmeshVertices() const
{
// Return number of vertices of the mesh representation
Int_t n;
n = fNseg+1;
Int_t nz = fNz+1;
Int_t numPoints = 2*n*nz;
return numPoints;
}
//_____________________________________________________________________________
void TGeoSphere::Sizeof3D() const
{
///// fill size of this 3-D object
/// TVirtualGeoPainter *painter = gGeoManager->GetGeomPainter();
/// if (!painter) return;
///
/// Int_t n;
/// n = fNseg+1;
/// Int_t nz = fNz+1;
/// Bool_t specialCase = kFALSE;
///
/// if (TMath::Abs(TMath::Sin(2*(fPhi2 - fPhi1))) <= 0.01) //mark this as a very special case, when
/// specialCase = kTRUE; //we have to draw this PCON like a TUBE
///
/// Int_t numPoints = 2*n*nz;
/// Int_t numSegs = 4*(nz*n-1+(specialCase == kTRUE));
/// Int_t numPolys = 2*(nz*n-1+(specialCase == kTRUE));
/// painter->AddSize3D(numPoints, numSegs, numPolys);
}
const TBuffer3D & TGeoSphere::GetBuffer3D(Int_t reqSections, Bool_t localFrame) const
{
static TBuffer3DSphere buffer;
TGeoBBox::FillBuffer3D(buffer, reqSections, localFrame);
if (reqSections & TBuffer3D::kShapeSpecific) {
buffer.fRadiusInner = fRmin;
buffer.fRadiusOuter = fRmax;
buffer.fThetaMin = fTheta1;
buffer.fThetaMax = fTheta2;
buffer.fPhiMin = fPhi1;
buffer.fPhiMax = fPhi2;
buffer.SetSectionsValid(TBuffer3D::kShapeSpecific);
}
if (reqSections & TBuffer3D::kRawSizes) {
// We want FillBuffer to be const
TGeoSphere * localThis = const_cast<TGeoSphere *>(this);
localThis->SetNumberOfDivisions(gGeoManager->GetNsegments());
Int_t n = GetNumberOfDivisions()+1;
Int_t nz = GetNz()+1;
Int_t NbPnts = 2*n*nz;
if (nz < 2 || NbPnts <= 0) {
assert(kFALSE);
}
else {
Bool_t specialCase = (TMath::Abs(TMath::Sin(2*(fPhi2 - fPhi1))) <= 0.01);
Int_t NbSegs = 4*(nz*n-1+(specialCase == kTRUE));
Int_t NbPols = 2*(nz*n-1+(specialCase == kTRUE));
if (buffer.SetRawSizes(NbPnts, 3*NbPnts, NbSegs, 3*NbSegs, NbPols, 6*NbPols)) {
buffer.SetSectionsValid(TBuffer3D::kRawSizes);
}
}
}
if ((reqSections & TBuffer3D::kRaw) && buffer.SectionsValid(TBuffer3D::kRawSizes)) {
SetPoints(buffer.fPnts);
if (!buffer.fLocalFrame) {
TransformPoints(buffer.fPnts, buffer.NbPnts());
}
SetSegsAndPols(buffer);
buffer.SetSectionsValid(TBuffer3D::kRaw);
}
return buffer;
}
ROOT page - Class index - Class Hierarchy - Top of the page
This page has been automatically generated. If you have any comments or suggestions about the page layout send a mail to ROOT support, or contact the developers with any questions or problems regarding ROOT.
 */
//
#include "Riostream.h"
#include "TROOT.h"
#include "TGeoCone.h"
#include "TGeoManager.h"
#include "TGeoVolume.h"
#include "TVirtualGeoPainter.h"
#include "TGeoSphere.h"
#include "TVirtualPad.h"
#include "TBuffer3D.h"
#include "TBuffer3DTypes.h"
ClassImp(TGeoSphere)
//_____________________________________________________________________________
TGeoSphere::TGeoSphere()
{
// Default constructor
SetShapeBit(TGeoShape::kGeoSph);
fNz = 0;
fNseg = 0;
fRmin = 0.0;
fRmax = 0.0;
fTheta1 = 0.0;
fTheta2 = 180.0;
fPhi1 = 0.0;
fPhi2 = 360.0;
}
//_____________________________________________________________________________
TGeoSphere::TGeoSphere(Double_t rmin, Double_t rmax, Double_t theta1,
Double_t theta2, Double_t phi1, Double_t phi2)
:TGeoBBox(0, 0, 0)
{
// Default constructor specifying minimum and maximum radius
SetShapeBit(TGeoShape::kGeoSph);
SetSphDimensions(rmin, rmax, theta1, theta2, phi1, phi2);
ComputeBBox();
SetNumberOfDivisions(20);
}
//_____________________________________________________________________________
TGeoSphere::TGeoSphere(const char *name, Double_t rmin, Double_t rmax, Double_t theta1,
Double_t theta2, Double_t phi1, Double_t phi2)
:TGeoBBox(name, 0, 0, 0)
{
// Default constructor specifying minimum and maximum radius
SetShapeBit(TGeoShape::kGeoSph);
SetSphDimensions(rmin, rmax, theta1, theta2, phi1, phi2);
ComputeBBox();
SetNumberOfDivisions(20);
}
//_____________________________________________________________________________
TGeoSphere::TGeoSphere(Double_t *param, Int_t /*nparam*/)
:TGeoBBox(0, 0, 0)
{
// Default constructor specifying minimum and maximum radius
// param[0] = Rmin
// param[1] = Rmax
SetShapeBit(TGeoShape::kGeoSph);
SetDimensions(param);
ComputeBBox();
SetNumberOfDivisions(20);
}
//_____________________________________________________________________________
TGeoSphere::~TGeoSphere()
{
// destructor
}
//_____________________________________________________________________________
void TGeoSphere::ComputeBBox()
{
// compute bounding box of the sphere
// Double_t xmin, xmax, ymin, ymax, zmin, zmax;
if (TMath::Abs(fTheta2-fTheta1) == 180) {
if (TMath::Abs(fPhi2-fPhi1) == 360) {
TGeoBBox::SetBoxDimensions(fRmax, fRmax, fRmax);
memset(fOrigin, 0, 3*sizeof(Double_t));
return;
}
}
Double_t st1 = TMath::Sin(fTheta1*TMath::DegToRad());
Double_t st2 = TMath::Sin(fTheta2*TMath::DegToRad());
Double_t r1min, r1max, r2min, r2max, rmin, rmax;
r1min = TMath::Min(fRmax*st1, fRmax*st2);
r1max = TMath::Max(fRmax*st1, fRmax*st2);
r2min = TMath::Min(fRmin*st1, fRmin*st2);
r2max = TMath::Max(fRmin*st1, fRmin*st2);
if (((fTheta1<=90) && (fTheta2>=90)) || ((fTheta2<=90) && (fTheta1>=90))) {
r1max = fRmax;
r2max = fRmin;
}
rmin = TMath::Min(r1min, r2min);
rmax = TMath::Max(r1max, r2max);
Double_t xc[4];
Double_t yc[4];
xc[0] = rmax*TMath::Cos(fPhi1*TMath::DegToRad());
yc[0] = rmax*TMath::Sin(fPhi1*TMath::DegToRad());
xc[1] = rmax*TMath::Cos(fPhi2*TMath::DegToRad());
yc[1] = rmax*TMath::Sin(fPhi2*TMath::DegToRad());
xc[2] = rmin*TMath::Cos(fPhi1*TMath::DegToRad());
yc[2] = rmin*TMath::Sin(fPhi1*TMath::DegToRad());
xc[3] = rmin*TMath::Cos(fPhi2*TMath::DegToRad());
yc[3] = rmin*TMath::Sin(fPhi2*TMath::DegToRad());
Double_t xmin = xc[TMath::LocMin(4, &xc[0])];
Double_t xmax = xc[TMath::LocMax(4, &xc[0])];
Double_t ymin = yc[TMath::LocMin(4, &yc[0])];
Double_t ymax = yc[TMath::LocMax(4, &yc[0])];
Double_t dp = fPhi2-fPhi1;
if (dp<0) dp+=360;
Double_t ddp = -fPhi1;
if (ddp<0) ddp+= 360;
if (ddp>360) ddp-=360;
if (ddp<=dp) xmax = rmax;
ddp = 90-fPhi1;
if (ddp<0) ddp+= 360;
if (ddp>360) ddp-=360;
if (ddp<=dp) ymax = rmax;
ddp = 180-fPhi1;
if (ddp<0) ddp+= 360;
if (ddp>360) ddp-=360;
if (ddp<=dp) xmin = -rmax;
ddp = 270-fPhi1;
if (ddp<0) ddp+= 360;
if (ddp>360) ddp-=360;
if (ddp<=dp) ymin = -rmax;
xc[0] = fRmax*TMath::Cos(fTheta1*TMath::DegToRad());
xc[1] = fRmax*TMath::Cos(fTheta2*TMath::DegToRad());
xc[2] = fRmin*TMath::Cos(fTheta1*TMath::DegToRad());
xc[3] = fRmin*TMath::Cos(fTheta2*TMath::DegToRad());
Double_t zmin = xc[TMath::LocMin(4, &xc[0])];
Double_t zmax = xc[TMath::LocMax(4, &xc[0])];
fOrigin[0] = (xmax+xmin)/2;
fOrigin[1] = (ymax+ymin)/2;
fOrigin[2] = (zmax+zmin)/2;;
fDX = (xmax-xmin)/2;
fDY = (ymax-ymin)/2;
fDZ = (zmax-zmin)/2;
}
//_____________________________________________________________________________
void TGeoSphere::ComputeNormal(Double_t *point, Double_t *dir, Double_t *norm)
{
// Compute normal to closest surface from POINT.
Double_t rxy2 = point[0]*point[0]+point[1]*point[1];
Double_t r2 = rxy2+point[2]*point[2];
Double_t r=TMath::Sqrt(r2);
Bool_t rzero=kFALSE;
if (r<=1E-20) rzero=kTRUE;
//localize theta
Double_t phi=0;
Double_t th=0.;
if (!rzero) th = TMath::ACos(point[2]/r);
//localize phi
phi=TMath::ATan2(point[1], point[0]);
Double_t saf[4];
saf[0]=(fRmin==0 && !TestShapeBit(kGeoThetaSeg) && !TestShapeBit(kGeoPhiSeg))?TGeoShape::Big():TMath::Abs(r-fRmin);
saf[1]=TMath::Abs(fRmax-r);
saf[2]=saf[3]= TGeoShape::Big();
if (TestShapeBit(kGeoThetaSeg)) {
if (fTheta1>0) {
saf[2] = r*TMath::Abs(TMath::Sin(th-fTheta1*TMath::DegToRad()));
}
if (fTheta2<180) {
saf[3] = r*TMath::Abs(TMath::Sin(fTheta2*TMath::DegToRad()-th));
}
}
Int_t i = TMath::LocMin(4,saf);
if (TestShapeBit(kGeoPhiSeg)) {
Double_t c1 = TMath::Cos(fPhi1*TMath::DegToRad());
Double_t s1 = TMath::Sin(fPhi1*TMath::DegToRad());
Double_t c2 = TMath::Cos(fPhi2*TMath::DegToRad());
Double_t s2 = TMath::Sin(fPhi2*TMath::DegToRad());
if (TGeoShape::IsCloseToPhi(saf[i], point,c1,s1,c2,s2)) {
TGeoShape::NormalPhi(point,dir,norm,c1,s1,c2,s2);
return;
}
}
if (i>1) {
if (i==2) th=(fTheta1<90)?(fTheta1+90):(fTheta1-90);
else th=(fTheta2<90)?(fTheta2+90):(fTheta2-90);
th *= TMath::DegToRad();
}
norm[0] = TMath::Sin(th)*TMath::Cos(phi);
norm[1] = TMath::Sin(th)*TMath::Sin(phi);
norm[2] = TMath::Cos(th);
if (norm[0]*dir[0]+norm[1]*dir[1]+norm[2]*dir[2]<0) {
norm[0] = -norm[0];
norm[1] = -norm[1];
norm[2] = -norm[2];
}
}
//_____________________________________________________________________________
Bool_t TGeoSphere::IsPointInside(Double_t *point, Bool_t checkR, Bool_t checkTh, Bool_t checkPh) const
{
Double_t r2 = point[0]*point[0]+point[1]*point[1]+point[2]*point[2];
if (checkR) {
if (TestShapeBit(kGeoRSeg) && (r2<fRmin*fRmin)) return kFALSE;
if (r2>fRmax*fRmax) return kFALSE;
}
if (r2<1E-20) return kTRUE;
if (checkPh && TestShapeBit(kGeoPhiSeg)) {
Double_t phi = TMath::ATan2(point[1], point[0]) * TMath::RadToDeg();
while (phi < fPhi1) phi+=360.;
Double_t dphi = fPhi2 -fPhi1;
Double_t ddp = phi - fPhi1;
if (ddp > dphi) return kFALSE;
}
if (checkTh && TestShapeBit(kGeoThetaSeg)) {
r2=TMath::Sqrt(r2);
// check theta range
Double_t theta = TMath::ACos(point[2]/r2)*TMath::RadToDeg();
if ((theta<fTheta1) || (theta>fTheta2)) return kFALSE;
}
return kTRUE;
}
//_____________________________________________________________________________
Bool_t TGeoSphere::Contains(Double_t *point) const
{
// test if point is inside this sphere
// check Rmin<=R<=Rmax
Double_t r2=point[0]*point[0]+point[1]*point[1]+point[2]*point[2];
if (TestShapeBit(kGeoRSeg) && (r2<fRmin*fRmin)) return kFALSE;
if (r2>fRmax*fRmax) return kFALSE;
if (r2<1E-20) return kTRUE;
// check phi range
if (TestShapeBit(kGeoPhiSeg)) {
Double_t phi = TMath::ATan2(point[1], point[0]) * TMath::RadToDeg();
if (phi < 0 ) phi+=360.;
Double_t dphi = fPhi2 -fPhi1;
if (dphi < 0) dphi+=360.;
Double_t ddp = phi - fPhi1;
if (ddp < 0) ddp += 360.;
if (ddp > dphi) return kFALSE;
}
if (TestShapeBit(kGeoThetaSeg)) {
r2=TMath::Sqrt(r2);
// check theta range
Double_t theta = TMath::ACos(point[2]/r2)*TMath::RadToDeg();
if ((theta<fTheta1) || (theta>fTheta2)) return kFALSE;
}
return kTRUE;
}
//_____________________________________________________________________________
Int_t TGeoSphere::DistancetoPrimitive(Int_t px, Int_t py)
{
// compute closest distance from point px,py to each corner
Int_t n = fNseg+1;
Int_t nz = fNz+1;
const Int_t numPoints = 2*n*nz;
return ShapeDistancetoPrimitive(numPoints, px, py);
}
//_____________________________________________________________________________
Double_t TGeoSphere::DistFromOutside(Double_t *point, Double_t *dir, Int_t iact, Double_t step, Double_t *safe) const
{
// compute distance from outside point to surface of the sphere
Double_t saf[6];
Double_t rxy2 = point[0]*point[0]+point[1]*point[1];
Double_t rxy = TMath::Sqrt(rxy2);
Double_t r2 = rxy2+point[2]*point[2];
Double_t r=TMath::Sqrt(r2);
Bool_t rzero=kFALSE;
Double_t phi=0;;
if (r<1E-20) rzero=kTRUE;
//localize theta
Double_t th=0.;
if (TestShapeBit(kGeoThetaSeg) && (!rzero)) {
th = TMath::ACos(point[2]/r)*TMath::RadToDeg();
}
//localize phi
if (TestShapeBit(kGeoPhiSeg)) {
phi=TMath::ATan2(point[1], point[0])*TMath::RadToDeg();
if (phi<0) phi+=360.;
}
if (iact<3 && safe) {
saf[0]=(r<fRmin)?fRmin-r:TGeoShape::Big();
saf[1]=(r>fRmax)?(r-fRmax):TGeoShape::Big();
saf[2]=saf[3]=saf[4]=saf[5]= TGeoShape::Big();
if (TestShapeBit(kGeoThetaSeg)) {
if (th < fTheta1) {
saf[2] = r*TMath::Sin((fTheta1-th)*TMath::DegToRad());
}
if (th > fTheta2) {
saf[3] = r*TMath::Sin((th-fTheta2)*TMath::DegToRad());
}
}
if (TestShapeBit(kGeoPhiSeg)) {
Double_t dph1=phi-fPhi1;
if (dph1<0) dph1+=360.;
if (dph1<=90.) saf[4]=rxy*TMath::Sin(dph1*TMath::DegToRad());
Double_t dph2=fPhi2-phi;
if (dph2<0) dph2+=360.;
if (dph2>90.) saf[5]=rxy*TMath::Sin(dph2*TMath::DegToRad());
}
*safe = saf[TMath::LocMin(6, &saf[0])];
if (iact==0) return TGeoShape::Big();
if (iact==1 && step<*safe) return TGeoShape::Big();
}
// compute distance to shape
Double_t snxt = TGeoShape::Big();
Double_t rdotn = point[0]*dir[0]+point[1]*dir[1]+point[2]*dir[2];
Bool_t fullsph = (!TestShapeBit(kGeoThetaSeg) && !TestShapeBit(kGeoPhiSeg))?kTRUE:kFALSE;
if (fullsph) {
Bool_t inrmax = kFALSE;
Bool_t inrmin = kFALSE;
if (r<=fRmax+TGeoShape::Tolerance()) inrmax = kTRUE;
if (r>=fRmin-TGeoShape::Tolerance()) inrmin = kTRUE;
if (inrmax && inrmin) {
if ((fRmax-r) < (r-fRmin)) {
// close to Rmax
if (rdotn>=0) return TGeoShape::Big();
return 0.0; // already in
}
// close to Rmin
if (fRmin==0.0 || rdotn>=0) return 0.0;
// check second crossing of Rmin
return DistToSphere(point, dir, fRmin, kFALSE, kFALSE);
}
}
// first check if any crossing at all
if (r>fRmax) {
Double_t b = rdotn;
Double_t c = r2-fRmax*fRmax;
Double_t d=b*b-c;
if (d<0) return TGeoShape::Big();
}
// do rmin, rmax, checking phi and theta ranges
if (r<fRmin) {
// check first cross of rmin
snxt = DistToSphere(point, dir, fRmin, kTRUE);
if (snxt<1E20) return snxt;
} else {
if (r>fRmax) {
// point outside rmax, check first cross of rmax
snxt = DistToSphere(point, dir, fRmax, kTRUE);
if (snxt<1E20) return snxt;
// now check first crossing of rmin
if (fRmin>0) {
snxt = DistToSphere(point, dir, fRmin, kTRUE);
// if this is outside range, check second crossing of rmin
if (snxt>1E20) {
snxt = DistToSphere(point, dir, fRmin, kTRUE, kFALSE);
if (snxt<1E20) return snxt;
}
}
} else {
// point between rmin and rmax, check first cross of rmin
snxt = DistToSphere(point, dir, fRmin, kTRUE);
// if this is outside range, check second crossing of rmin
if (snxt>1E20) {
snxt = DistToSphere(point, dir, fRmin, kTRUE, kFALSE);
if (snxt<1E20) return snxt;
}
}
}
// check theta conical surfaces
Double_t ptnew[3];
Double_t b,delta, znew;
Double_t st1=TGeoShape::Big(), st2=TGeoShape::Big();
if (TestShapeBit(kGeoThetaSeg)) {
if (fTheta1>0) {
if (fTheta1==90) {
// surface is a plane
if (point[2]*dir[2]<0) {
snxt = -point[2]/dir[2];
ptnew[0] = point[0]+snxt*dir[0];
ptnew[1] = point[1]+snxt*dir[1];
ptnew[2] = 0;
// check range
if (IsPointInside(&ptnew[0], kTRUE, kFALSE, kTRUE)) return snxt;
}
} else {
Double_t r1,r2,z1,z2,dz;
Double_t si = TMath::Sin(fTheta1*TMath::DegToRad());
Double_t ci = TMath::Cos(fTheta1*TMath::DegToRad());
if (ci>0) {
r1 = fRmin*si;
z1 = fRmin*ci;
r2 = fRmax*si;
z2 = fRmax*ci;
} else {
r1 = fRmax*si;
z1 = fRmax*ci;
r2 = fRmin*si;
z2 = fRmin*ci;
}
dz = 0.5*(z2-z1);
ptnew[0] = point[0];
ptnew[1] = point[1];
ptnew[2] = point[2]-0.5*(z1+z2);
if (TestShapeBit(kGeoPhiSeg)) {
st1 = TGeoConeSeg::DistToCons(point, dir, r1, z1, r2, z2, fPhi1, fPhi2);
} else {
TGeoCone::DistToCone(ptnew, dir, dz, r1, r2, b, delta);
if (delta>0) {
st1 = -b-delta;
znew = ptnew[2]+st1*dir[2];
if (st1<0 || TMath::Abs(znew)>0) {
st1 = -b+delta;
znew = ptnew[2]+st1*dir[2];
if (st1<0 || TMath::Abs(znew)>0) st1=TGeoShape::Big();
}
}
}
}
}
if (fTheta2<180) {
if (fTheta2==90) {
// surface is a plane
if (point[2]*dir[2]<0) {
snxt = -point[2]/dir[2];
ptnew[0] = point[0]+snxt*dir[0];
ptnew[1] = point[1]+snxt*dir[1];
ptnew[2] = 0;
// check range
if (IsPointInside(&ptnew[0], kTRUE, kFALSE, kTRUE)) return snxt;
}
} else {
Double_t r1,r2,z1,z2,dz;
Double_t si = TMath::Sin(fTheta2*TMath::DegToRad());
Double_t ci = TMath::Cos(fTheta2*TMath::DegToRad());
if (ci>0) {
r1 = fRmin*si;
z1 = fRmin*ci;
r2 = fRmax*si;
z2 = fRmax*ci;
} else {
r1 = fRmax*si;
z1 = fRmax*ci;
r2 = fRmin*si;
z2 = fRmin*ci;
}
dz = 0.5*(z2-z1);
ptnew[0] = point[0];
ptnew[1] = point[1];
ptnew[2] = point[2]-0.5*(z1+z2);
if (TestShapeBit(kGeoPhiSeg)) {
st2 = TGeoConeSeg::DistToCons(point, dir, r1, z1, r2, z2, fPhi1, fPhi2);
} else {
TGeoCone::DistToCone(ptnew, dir, dz, r1, r2, b, delta);
if (delta>0) {
st2 = -b-delta;
znew = ptnew[2]+st2*dir[2];
if (st2<0 || TMath::Abs(znew)>dz) {
st2 = -b+delta;
znew = ptnew[2]+st2*dir[2];
if (st2<0 || TMath::Abs(znew)>0) st2=TGeoShape::Big();
}
}
}
}
}
}
snxt = TMath::Min(st1, st2);
// if (snxt<1E20) return snxt;
if (TestShapeBit(kGeoPhiSeg)) {
Double_t s1 = TMath::Sin(fPhi1*TMath::DegToRad());
Double_t c1 = TMath::Cos(fPhi1*TMath::DegToRad());
Double_t s2 = TMath::Sin(fPhi2*TMath::DegToRad());
Double_t c2 = TMath::Cos(fPhi2*TMath::DegToRad());
Double_t phim = 0.5*(fPhi1+fPhi2);
Double_t sm = TMath::Sin(phim*TMath::DegToRad());
Double_t cm = TMath::Cos(phim*TMath::DegToRad());
Double_t sfi1=TGeoShape::Big();
Double_t sfi2=TGeoShape::Big();
Double_t s=0;
Double_t safety, un;
safety = point[0]*s1-point[1]*c1;
if (safety>0) {
un = dir[0]*s1-dir[1]*c1;
if (un<0) {
s=-safety/un;
ptnew[0] = point[0]+s*dir[0];
ptnew[1] = point[1]+s*dir[1];
ptnew[2] = point[2]+s*dir[2];
if ((ptnew[1]*cm-ptnew[0]*sm)<=0) {
sfi1=s;
if (IsPointInside(&ptnew[0], kTRUE, kTRUE, kFALSE) && sfi1<snxt) return sfi1;
}
}
}
safety = -point[0]*s2+point[1]*c2;
if (safety>0) {
un = -dir[0]*s2+dir[1]*c2;
if (un<0) {
s=-safety/un;
ptnew[0] = point[0]+s*dir[0];
ptnew[1] = point[1]+s*dir[1];
ptnew[2] = point[2]+s*dir[2];
if ((ptnew[1]*cm-ptnew[0]*sm)>=0) {
sfi2=s;
if (IsPointInside(&ptnew[0], kTRUE, kTRUE, kFALSE) && sfi2<snxt) return sfi2;
}
}
}
}
return snxt;
}
//_____________________________________________________________________________
Double_t TGeoSphere::DistFromInside(Double_t *point, Double_t *dir, Int_t iact, Double_t step, Double_t *safe) const
{
// compute distance from inside point to surface of the sphere
Double_t saf[6];
Double_t rxy2 = point[0]*point[0]+point[1]*point[1];
Double_t rxy = TMath::Sqrt(rxy2);
Double_t r2 = rxy2+point[2]*point[2];
Double_t r=TMath::Sqrt(r2);
Bool_t rzero=kFALSE;
if (r<=1E-20) rzero=kTRUE;
//localize theta
Double_t phi=0;;
Double_t th=0.;
if (TestShapeBit(kGeoThetaSeg) && (!rzero)) {
th = TMath::ACos(point[2]/r)*TMath::RadToDeg();
}
//localize phi
if (TestShapeBit(kGeoPhiSeg)) {
phi=TMath::ATan2(point[1], point[0])*TMath::RadToDeg();
if (phi<0) phi+=360.;
}
if (iact<3 && safe) {
saf[0]=(fRmin==0)?TGeoShape::Big():r-fRmin;
saf[1]=fRmax-r;
saf[2]=saf[3]=saf[4]=saf[5]= TGeoShape::Big();
if (TestShapeBit(kGeoThetaSeg)) {
if (fTheta1>0) {
saf[2] = r*TMath::Sin((th-fTheta1)*TMath::DegToRad());
}
if (fTheta2<180) {
saf[3] = r*TMath::Sin((fTheta2-th)*TMath::DegToRad());
}
}
if (TestShapeBit(kGeoPhiSeg)) {
Double_t dph1=phi-fPhi1;
if (dph1<0) dph1+=360.;
if (dph1<=90.) saf[4]=rxy*TMath::Sin(dph1*TMath::DegToRad());
Double_t dph2=fPhi2-phi;
if (dph2<0) dph2+=360.;
if (dph2<=90.) saf[5]=rxy*TMath::Sin(dph2*TMath::DegToRad());
}
*safe = saf[TMath::LocMin(6, &saf[0])];
if (iact==0) return TGeoShape::Big();
if (iact==1 && step<*safe) return TGeoShape::Big();
}
// compute distance to shape
Double_t snxt = TGeoShape::Big();
if (rzero) {
// gGeoManager->SetNormalChecked(1.);
return fRmax;
}
// first do rmin, rmax
Double_t b,delta, znew;
Double_t rdotn = point[0]*dir[0]+point[1]*dir[1]+point[2]*dir[2];
Double_t sn1 = TGeoShape::Big();
// Inner sphere
if (fRmin>0) {
// Protection in case point is actually outside the sphere
if (r <= fRmin+TGeoShape::Tolerance()) {
if (rdotn<0) return 0.0;
} else {
if (rdotn<0) sn1 = DistToSphere(point, dir, fRmin, kFALSE);
}
}
Double_t sn2 = TGeoShape::Big();
// Outer sphere
if (r >= fRmax-TGeoShape::Tolerance()) {
if (rdotn>=0) return 0.0;
}
sn2 = DistToSphere(point, dir, fRmax, kFALSE);
Double_t sr = TMath::Min(sn1, sn2);
// check theta conical surfaces
sn1 = TGeoShape::Big();
sn2 = TGeoShape::Big();
if (TestShapeBit(kGeoThetaSeg)) {
if (fTheta1==90) {
// surface is a plane
if (point[2]*dir[2]<0) sn1 = -point[2]/dir[2];
} else {
if (fTheta1>0) {
Double_t r1,r2,z1,z2,dz,ptnew[3];
Double_t si = TMath::Sin(fTheta1*TMath::DegToRad());
Double_t ci = TMath::Cos(fTheta1*TMath::DegToRad());
if (ci>0) {
r1 = fRmin*si;
z1 = fRmin*ci;
r2 = fRmax*si;
z2 = fRmax*ci;
} else {
r1 = fRmax*si;
z1 = fRmax*ci;
r2 = fRmin*si;
z2 = fRmin*ci;
}
dz = 0.5*(z2-z1);
ptnew[0] = point[0];
ptnew[1] = point[1];
ptnew[2] = point[2]-0.5*(z1+z2);
if (TestShapeBit(kGeoPhiSeg)) {
sn1 = TGeoConeSeg::DistToCons(point, dir, r1, z1, r2, z2, fPhi1, fPhi2);
} else {
TGeoCone::DistToCone(ptnew, dir, dz, r1, r2, b, delta);
if (delta>0) {
sn1 = -b-delta;
znew = ptnew[2]+sn1*dir[2];
if (sn1<0 || TMath::Abs(znew)>dz) {
sn1 = -b+delta;
znew = ptnew[2]+sn1*dir[2];
if (sn1<0 || TMath::Abs(znew)>0) sn1=TGeoShape::Big();
}
}
}
}
}
if (fTheta2==90) {
// surface is a plane
if (point[2]*dir[2]<0) sn1 = -point[2]/dir[2];
} else {
if (fTheta2<180) {
Double_t r1,r2,z1,z2,dz,ptnew[3];
Double_t si = TMath::Sin(fTheta2*TMath::DegToRad());
Double_t ci = TMath::Cos(fTheta2*TMath::DegToRad());
if (ci>0) {
r1 = fRmin*si;
z1 = fRmin*ci;
r2 = fRmax*si;
z2 = fRmax*ci;
} else {
r1 = fRmax*si;
z1 = fRmax*ci;
r2 = fRmin*si;
z2 = fRmin*ci;
}
dz = 0.5*(z2-z1);
ptnew[0] = point[0];
ptnew[1] = point[1];
ptnew[2] = point[2]-0.5*(z1+z2);
if (TestShapeBit(kGeoPhiSeg)) {
sn2 = TGeoConeSeg::DistToCons(point, dir, r1, z1, r2, z2, fPhi1, fPhi2);
} else {
TGeoCone::DistToCone(ptnew, dir, dz, r1, r2, b, delta);
if (delta>0) {
sn2 = -b-delta;
znew = ptnew[2]+sn2*dir[2];
if (sn2<0 || TMath::Abs(znew)>0) {
sn2 = -b+delta;
znew = ptnew[2]+sn2*dir[2];
if (sn2<0 || TMath::Abs(znew)>0) sn2=TGeoShape::Big();
}
}
}
}
}
}
Double_t st = TMath::Min(sn1,sn2);
Double_t sp = TGeoShape::Big();
if (TestShapeBit(kGeoPhiSeg)) {
Double_t s1 = TMath::Sin(fPhi1*TMath::DegToRad());
Double_t c1 = TMath::Cos(fPhi1*TMath::DegToRad());
Double_t s2 = TMath::Sin(fPhi2*TMath::DegToRad());
Double_t c2 = TMath::Cos(fPhi2*TMath::DegToRad());
Double_t phim = 0.5*(fPhi1+fPhi2);
Double_t sm = TMath::Sin(phim*TMath::DegToRad());
Double_t cm = TMath::Cos(phim*TMath::DegToRad());
sp = TGeoShape::DistToPhiMin(point, dir, s1, c1, s2, c2, sm, cm);
}
snxt = TMath::Min(sr, st);
snxt = TMath::Min(snxt, sp);
return snxt;
}
//_____________________________________________________________________________
Double_t TGeoSphere::DistToSphere(Double_t *point, Double_t *dir, Double_t rsph, Bool_t check, Bool_t firstcross) const
{
// compute distance to sphere of radius rsph. Direction has to be a unit vector
if (rsph<=0) return TGeoShape::Big();
Double_t s=TGeoShape::Big();
Double_t r2 = point[0]*point[0]+point[1]*point[1]+point[2]*point[2];
Double_t b = point[0]*dir[0]+point[1]*dir[1]+point[2]*dir[2];
Double_t c = r2-rsph*rsph;
Bool_t in = (c<=0)?kTRUE:kFALSE;
Double_t d;
d=b*b-c;
if (d<0) return TGeoShape::Big();
Double_t pt[3];
Int_t i;
d = TMath::Sqrt(d);
if (in) {
s=-b+d;
} else {
s = (firstcross)?(-b-d):(-b+d);
}
if (s<0) return TGeoShape::Big();
if (!check) return s;
for (i=0; i<3; i++) pt[i]=point[i]+s*dir[i];
// check theta and phi ranges
if (IsPointInside(&pt[0], kFALSE)) return s;
return TGeoShape::Big();
}
//_____________________________________________________________________________
TGeoVolume *TGeoSphere::Divide(TGeoVolume * /*voldiv*/, const char * /*divname*/, Int_t /*iaxis*/, Int_t /*ndiv*/,
Double_t /*start*/, Double_t /*step*/)
{
// Divide all range of iaxis in range/step cells
Error("Divide", "Division of a sphere not implemented");
return 0;
}
//_____________________________________________________________________________
const char *TGeoSphere::GetAxisName(Int_t iaxis) const
{
// Returns name of axis IAXIS.
switch (iaxis) {
case 1:
return "R";
case 2:
return "THETA";
case 3:
return "PHI";
default:
return "UNDEFINED";
}
}
//_____________________________________________________________________________
Double_t TGeoSphere::GetAxisRange(Int_t iaxis, Double_t &xlo, Double_t &xhi) const
{
// Get range of shape for a given axis.
xlo = 0;
xhi = 0;
Double_t dx = 0;
switch (iaxis) {
case 1:
xlo = fRmin;
xhi = fRmax;
dx = xhi-xlo;
return dx;
case 2:
xlo = fPhi1;
xhi = fPhi2;
dx = xhi-xlo;
return dx;
case 3:
xlo = fTheta1;
xhi = fTheta2;
dx = xhi-xlo;
return dx;
}
return dx;
}
//_____________________________________________________________________________
void TGeoSphere::GetBoundingCylinder(Double_t *param) const
{
//--- Fill vector param[4] with the bounding cylinder parameters. The order
// is the following : Rmin, Rmax, Phi1, Phi2
Double_t smin = TMath::Sin(fTheta1*TMath::DegToRad());
Double_t smax = TMath::Sin(fTheta2*TMath::DegToRad());
if (smin>smax) {
Double_t a = smin;
smin = smax;
smax = a;
}
param[0] = fRmin*smin; // Rmin
param[0] *= param[0];
if (((90.-fTheta1)*(fTheta2-90.))>=0) smax = 1.;
param[1] = fRmax*smax; // Rmax
param[1] *= param[1];
param[2] = (fPhi1<0)?(fPhi1+360.):fPhi1; // Phi1
param[3] = fPhi2;
if ((param[3]-param[2])==360.) { // Phi2
param[2] = 0.;
param[3] = 360.;
}
while (param[3]<param[2]) param[3]+=360.;
}
//_____________________________________________________________________________
void TGeoSphere::InspectShape() const
{
// print shape parameters
printf("*** Shape %s: TGeoSphere ***\n", GetName());
printf(" Rmin = %11.5f\n", fRmin);
printf(" Rmax = %11.5f\n", fRmax);
printf(" Th1 = %11.5f\n", fTheta1);
printf(" Th2 = %11.5f\n", fTheta2);
printf(" Ph1 = %11.5f\n", fPhi1);
printf(" Ph2 = %11.5f\n", fPhi2);
printf(" Bounding box:\n");
TGeoBBox::InspectShape();
}
//_____________________________________________________________________________
TBuffer3D *TGeoSphere::MakeBuffer3D() const
{
// Creates a TBuffer3D describing *this* shape.
// Coordinates are in local reference frame.
Int_t n = gGeoManager->GetNsegments()+1;
Double_t ph1 = GetPhi1();
Double_t ph2 = GetPhi2();
Int_t nz = GetNz()+1;
if (nz < 2) return 0;
Int_t NbPnts = 2*n*nz;
if (NbPnts <= 0) return 0;
Bool_t specialCase = kFALSE;
if (TMath::Abs(TMath::Sin(2*(ph2 - ph1))) <= 0.01) specialCase = kTRUE;
Int_t NbSegs = 4*(nz*n-1+(specialCase == kTRUE));
Int_t NbPols = 2*(nz*n-1+(specialCase == kTRUE));
TBuffer3D* buff = new TBuffer3D(TBuffer3DTypes::kGeneric,
NbPnts, 3*NbPnts, NbSegs, 3*NbSegs, NbPols, 6*NbPols);
if (buff)
{
SetPoints(buff->fPnts);
SetSegsAndPols(*buff);
}
return buff;
}
//_____________________________________________________________________________
void TGeoSphere::SetSegsAndPols(TBuffer3D & buff) const
{
// Fill TBuffer3D structure for segments and polygons.
Int_t i, j;
Int_t n = gGeoManager->GetNsegments()+1;
Double_t ph1 = GetPhi1();
Double_t ph2 = GetPhi2();
Int_t nz = GetNz()+1;
if (nz < 2) return;
Bool_t specialCase = kFALSE;
if (TMath::Abs(TMath::Sin(2*(ph2 - ph1))) <= 0.01) specialCase = kTRUE;
Int_t c = GetBasicColor();
Int_t indx, indx2, k;
indx = indx2 = 0;
//inside & outside spheres, number of segments: 2*nz*(n-1)
// special case number of segments: 2*nz*n
for (i = 0; i < nz*2; i++) {
indx2 = i*n;
for (j = 1; j < n; j++) {
buff.fSegs[indx++] = c;
buff.fSegs[indx++] = indx2+j-1;
buff.fSegs[indx++] = indx2+j;
}
if (specialCase) {
buff.fSegs[indx++] = c;
buff.fSegs[indx++] = indx2+j-1;
buff.fSegs[indx++] = indx2;
}
}
//bottom & top lines, number of segments: 2*n
for (i = 0; i < 2; i++) {
indx2 = i*(nz-1)*2*n;
for (j = 0; j < n; j++) {
buff.fSegs[indx++] = c;
buff.fSegs[indx++] = indx2+j;
buff.fSegs[indx++] = indx2+n+j;
}
}
//inside & outside spheres, number of segments: 2*(nz-1)*n
for (i = 0; i < (nz-1); i++) {
//inside sphere
indx2 = i*n*2;
for (j = 0; j < n; j++) {
buff.fSegs[indx++] = c+2;
buff.fSegs[indx++] = indx2+j;
buff.fSegs[indx++] = indx2+n*2+j;
}
//outside sphere
indx2 = i*n*2+n;
for (j = 0; j < n; j++) {
buff.fSegs[indx++] = c+3;
buff.fSegs[indx++] = indx2+j;
buff.fSegs[indx++] = indx2+n*2+j;
}
}
//left & right sections, number of segments: 2*(nz-2)
// special case number of segments: 0
if (!specialCase) {
for (i = 1; i < (nz-1); i++) {
for (j = 0; j < 2; j++) {
buff.fSegs[indx++] = c;
buff.fSegs[indx++] = 2*i * n + j*(n-1);
buff.fSegs[indx++] = (2*i+1) * n + j*(n-1);
}
}
}
Int_t m = n - 1 + (specialCase == kTRUE);
indx = 0;
//bottom & top, number of polygons: 2*(n-1)
// special case number of polygons: 2*n
i = 0;
for (j = 0; j < n-1; j++) {
buff.fPols[indx++] = c+3;
buff.fPols[indx++] = 4;
buff.fPols[indx++] = i*(nz*2-2)*m+j;
buff.fPols[indx++] = 2*nz*m+i*n+j+1;
buff.fPols[indx++] = i*(nz*2-2)*m+m+j;
buff.fPols[indx++] = 2*nz*m+i*n+j;
}
if (specialCase) {
buff.fPols[indx++] = c+3;
buff.fPols[indx++] = 4;
buff.fPols[indx++] = i*(nz*2-2)*m+j;
buff.fPols[indx++] = 2*nz*m+i*n;
buff.fPols[indx++] = i*(nz*2-2)*m+m+j;
buff.fPols[indx++] = 2*nz*m+i*n+j;
}
i = 1;
for (j = 0; j < n-1; j++) {
buff.fPols[indx++] = c+3;
buff.fPols[indx++] = 4;
buff.fPols[indx++] = 2*nz*m+i*n+j;
buff.fPols[indx++] = i*(nz*2-2)*m+m+j;
buff.fPols[indx++] = 2*nz*m+i*n+j+1;
buff.fPols[indx++] = i*(nz*2-2)*m+j;
}
if (specialCase) {
buff.fPols[indx++] = c+3;
buff.fPols[indx++] = 4;
buff.fPols[indx++] = 2*nz*m+i*n+j;
buff.fPols[indx++] = i*(nz*2-2)*m+m+j;
buff.fPols[indx++] = 2*nz*m+i*n;
buff.fPols[indx++] = i*(nz*2-2)*m+j;
}
//inside & outside, number of polygons: (nz-1)*2*(n-1)
for (k = 0; k < (nz-1); k++) {
i = 0;
for (j = 0; j < n-1; j++) {
buff.fPols[indx++] = c+i;
buff.fPols[indx++] = 4;
buff.fPols[indx++] = (2*k+i*1)*m+j;
buff.fPols[indx++] = nz*2*m+(2*k+i*1+2)*n+j;
buff.fPols[indx++] = (2*k+i*1+2)*m+j;
buff.fPols[indx++] = nz*2*m+(2*k+i*1+2)*n+j+1;
}
if (specialCase) {
buff.fPols[indx++] = c+i;
buff.fPols[indx++] = 4;
buff.fPols[indx++] = (2*k+i*1)*m+j;
buff.fPols[indx++] = nz*2*m+(2*k+i*1+2)*n+j;
buff.fPols[indx++] = (2*k+i*1+2)*m+j;
buff.fPols[indx++] = nz*2*m+(2*k+i*1+2)*n;
}
i = 1;
for (j = 0; j < n-1; j++) {
buff.fPols[indx++] = c+i;
buff.fPols[indx++] = 4;
buff.fPols[indx++] = nz*2*m+(2*k+i*1+2)*n+j+1;
buff.fPols[indx++] = (2*k+i*1+2)*m+j;
buff.fPols[indx++] = nz*2*m+(2*k+i*1+2)*n+j;
buff.fPols[indx++] = (2*k+i*1)*m+j;
}
if (specialCase) {
buff.fPols[indx++] = c+i;
buff.fPols[indx++] = 4;
buff.fPols[indx++] = nz*2*m+(2*k+i*1+2)*n;
buff.fPols[indx++] = (2*k+i*1+2)*m+j;
buff.fPols[indx++] = nz*2*m+(2*k+i*1+2)*n+j;
buff.fPols[indx++] = (2*k+i*1)*m+j;
}
}
//left & right sections, number of polygons: 2*(nz-1)
// special case number of polygons: 0
if (!specialCase) {
indx2 = nz*2*(n-1);
for (k = 0; k < (nz-1); k++) {
i = 0;
buff.fPols[indx++] = c+2;
buff.fPols[indx++] = 4;
buff.fPols[indx++] = k==0 ? indx2+i*(n-1) : indx2+2*nz*n+2*(k-1)+i;
buff.fPols[indx++] = indx2+(2*k+3)*n+i*(n-1);
buff.fPols[indx++] = indx2+2*nz*n+2*k+i;
buff.fPols[indx++] = indx2+2*(k+1)*n+i*(n-1);
i = 1;
buff.fPols[indx++] = c+2;
buff.fPols[indx++] = 4;
buff.fPols[indx++] = k==0 ? indx2+i*(n-1) : indx2+2*nz*n+2*(k-1)+i;
buff.fPols[indx++] = indx2+2*(k+1)*n+i*(n-1);
buff.fPols[indx++] = indx2+2*nz*n+2*k+i;
buff.fPols[indx++] = indx2+(2*k+3)*n+i*(n-1);
}
buff.fPols[indx-8] = indx2+n;
buff.fPols[indx-2] = indx2+2*n-1;
}
}
//_____________________________________________________________________________
Double_t TGeoSphere::Safety(Double_t *point, Bool_t in) const
{
// computes the closest distance from given point to this shape, according
// to option. The matching point on the shape is stored in spoint.
Double_t r2 = point[0]*point[0]+point[1]*point[1]+point[2]*point[2];
Double_t r=TMath::Sqrt(r2);
Bool_t rzero=kFALSE;
if (r<=1E-20) rzero=kTRUE;
//localize theta
Double_t th=0.;
if (TestShapeBit(kGeoThetaSeg) && (!rzero)) {
th = TMath::ACos(point[2]/r)*TMath::RadToDeg();
}
Double_t saf[4];
saf[0]=(fRmin==0 && !TestShapeBit(kGeoThetaSeg) && !TestShapeBit(kGeoPhiSeg))?TGeoShape::Big():r-fRmin;
saf[1]=fRmax-r;
saf[2]=saf[3]= TGeoShape::Big();
if (TestShapeBit(kGeoThetaSeg)) {
if (fTheta1>0) saf[2] = r*TMath::Sin((th-fTheta1)*TMath::DegToRad());
if (fTheta2<180) saf[3] = r*TMath::Sin((fTheta2-th)*TMath::DegToRad());
}
Double_t safphi = TGeoShape::Big();
Double_t safe = TGeoShape::Big();
if (TestShapeBit(kGeoPhiSeg)) safphi = TGeoShape::SafetyPhi(point,in,fPhi1,fPhi2);
if (in) {
safe = saf[TMath::LocMin(4,saf)];
return TMath::Min(safe,safphi);
}
for (Int_t i=0; i<4; i++) saf[i]=-saf[i];
safe = saf[TMath::LocMax(4, saf)];
if (TestShapeBit(kGeoPhiSeg)) return TMath::Max(safe, safphi);
return safe;
}
//_____________________________________________________________________________
void TGeoSphere::SavePrimitive(ofstream &out, Option_t * /*option*/)
{
// Save a primitive as a C++ statement(s) on output stream "out".
if (TObject::TestBit(kGeoSavePrimitive)) return;
out << " // Shape: " << GetName() << " type: " << ClassName() << endl;
out << " rmin = " << fRmin << ";" << endl;
out << " rmax = " << fRmax << ";" << endl;
out << " theta1 = " << fTheta1<< ";" << endl;
out << " theta2 = " << fTheta2 << ";" << endl;
out << " phi1 = " << fPhi1 << ";" << endl;
out << " phi2 = " << fPhi2 << ";" << endl;
out << " TGeoShape *" << GetPointerName() << " = new TGeoSphere(\"" << GetName() << "\",rmin,rmax,theta1, theta2,phi1,phi2);" << endl;
TObject::SetBit(TGeoShape::kGeoSavePrimitive);
}
//_____________________________________________________________________________
void TGeoSphere::SetSphDimensions(Double_t rmin, Double_t rmax, Double_t theta1,
Double_t theta2, Double_t phi1, Double_t phi2)
{
if (rmin >= rmax) {
Error("SetDimensions", "invalid parameters rmin/rmax");
return;
}
fRmin = rmin;
fRmax = rmax;
if (rmin>0) SetShapeBit(kGeoRSeg);
if (theta1 >= theta2 || theta1<0 || theta1>180 || theta2>180) {
Error("SetDimensions", "invalid parameters theta1/theta2");
return;
}
fTheta1 = theta1;
fTheta2 = theta2;
if ((theta2-theta1)<180.) SetShapeBit(kGeoThetaSeg);
fPhi1 = phi1;
if (phi1<0) fPhi1+=360.;
fPhi2 = phi2;
while (fPhi2<fPhi1) fPhi2+=360.;
if (TMath::Abs(phi2-phi1)!=360.) SetShapeBit(kGeoPhiSeg);
}
//_____________________________________________________________________________
void TGeoSphere::SetDimensions(Double_t *param)
{
Double_t rmin = param[0];
Double_t rmax = param[1];
Double_t theta1 = 0;
Double_t theta2 = 180.;
Double_t phi1 = 0;
Double_t phi2 = 360.;
// if (nparam > 2) theta1 = param[2];
// if (nparam > 3) theta2 = param[3];
// if (nparam > 4) phi1 = param[4];
// if (nparam > 5) phi2 = param[5];
SetSphDimensions(rmin, rmax, theta1, theta2, phi1, phi2);
}
//_____________________________________________________________________________
void TGeoSphere::SetNumberOfDivisions(Int_t p)
{
fNseg = p;
Double_t dphi = fPhi2 - fPhi1;
if (dphi<0) dphi+=360;
Double_t dtheta = TMath::Abs(fTheta2-fTheta1);
fNz = Int_t(fNseg*dtheta/dphi) +1;
}
//_____________________________________________________________________________
void TGeoSphere::SetPoints(Double_t *points) const
{
// create sphere mesh points
Int_t i,j ;
if (points) {
Double_t dphi = fPhi2-fPhi1;
if (dphi<0) dphi+=360;
Double_t dtheta = fTheta2-fTheta1;
Int_t n = fNseg + 1;
dphi = dphi/fNseg;
dtheta = dtheta/fNz;
Double_t z, theta, phi, cphi, sphi;
Int_t indx=0;
for (i = 0; i < fNz+1; i++)
{
theta = (fTheta1+i*dtheta)*TMath::DegToRad();
z = fRmin * TMath::Cos(theta); // fSinPhiTab[i];
Double_t zi = fRmin*TMath::Sin(theta);
// printf("plane %i nseg=%i z=%f:\n", i,n,z);
for (j = 0; j < n; j++) {
phi = (fPhi1+j*dphi)*TMath::DegToRad();
cphi = TMath::Cos(phi);
sphi = TMath::Sin(phi);
points[indx++] = zi * cphi;
points[indx++] = zi * sphi;
points[indx++] = z;
// printf("%i %f %f %f\n", j, points[3*j], points[3*j+1], points[3*j+2]);
}
z = fRmax * TMath::Cos(theta);
zi = fRmax* TMath::Sin(theta);
// printf("outer points for plane %i:\n", i);
for (j = 0; j < n; j++) {
phi = (fPhi1+j*dphi)*TMath::DegToRad();
cphi = TMath::Cos(phi);
sphi = TMath::Sin(phi);
points[indx++] = zi * cphi;
points[indx++] = zi * sphi;
points[indx++] = z;
// printf("%i %f %f %f\n", j, points[n+3*j], points[n+3*j+1], points[n+3*j+2]);
}
}
}
}
//_____________________________________________________________________________
void TGeoSphere::SetPoints(Float_t *points) const
{
// create sphere mesh points
Int_t i,j ;
if (points) {
Double_t dphi = fPhi2-fPhi1;
if (dphi<0) dphi+=360;
Double_t dtheta = fTheta2-fTheta1;
Int_t n = fNseg + 1;
dphi = dphi/fNseg;
dtheta = dtheta/fNz;
Double_t z, theta, phi, cphi, sphi;
Int_t indx=0;
for (i = 0; i < fNz+1; i++)
{
theta = (fTheta1+i*dtheta)*TMath::DegToRad();
z = fRmin * TMath::Cos(theta); // fSinPhiTab[i];
Double_t zi = fRmin*TMath::Sin(theta);
// printf("plane %i nseg=%i z=%f:\n", i,n,z);
for (j = 0; j < n; j++)
{
phi = (fPhi1+j*dphi)*TMath::DegToRad();
cphi = TMath::Cos(phi);
sphi = TMath::Sin(phi);
points[indx++] = zi * cphi;
points[indx++] = zi * sphi;
points[indx++] = z;
// printf("%i %f %f %f\n", j, points[3*j], points[3*j+1], points[3*j+2]);
}
z = fRmax * TMath::Cos(theta);
zi = fRmax* TMath::Sin(theta);
// printf("outer points for plane %i:\n", i);
for (j = 0; j < n; j++)
{
phi = (fPhi1+j*dphi)*TMath::DegToRad();
cphi = TMath::Cos(phi);
sphi = TMath::Sin(phi);
points[indx++] = zi * cphi;
points[indx++] = zi * sphi;
points[indx++] = z;
// printf("%i %f %f %f\n", j, points[n+3*j], points[n+3*j+1], points[n+3*j+2]);
}
}
}
}
//_____________________________________________________________________________
Int_t TGeoSphere::GetNmeshVertices() const
{
// Return number of vertices of the mesh representation
Int_t n;
n = fNseg+1;
Int_t nz = fNz+1;
Int_t numPoints = 2*n*nz;
return numPoints;
}
//_____________________________________________________________________________
void TGeoSphere::Sizeof3D() const
{
///// fill size of this 3-D object
/// TVirtualGeoPainter *painter = gGeoManager->GetGeomPainter();
/// if (!painter) return;
///
/// Int_t n;
/// n = fNseg+1;
/// Int_t nz = fNz+1;
/// Bool_t specialCase = kFALSE;
///
/// if (TMath::Abs(TMath::Sin(2*(fPhi2 - fPhi1))) <= 0.01) //mark this as a very special case, when
/// specialCase = kTRUE; //we have to draw this PCON like a TUBE
///
/// Int_t numPoints = 2*n*nz;
/// Int_t numSegs = 4*(nz*n-1+(specialCase == kTRUE));
/// Int_t numPolys = 2*(nz*n-1+(specialCase == kTRUE));
/// painter->AddSize3D(numPoints, numSegs, numPolys);
}
const TBuffer3D & TGeoSphere::GetBuffer3D(Int_t reqSections, Bool_t localFrame) const
{
static TBuffer3DSphere buffer;
TGeoBBox::FillBuffer3D(buffer, reqSections, localFrame);
if (reqSections & TBuffer3D::kShapeSpecific) {
buffer.fRadiusInner = fRmin;
buffer.fRadiusOuter = fRmax;
buffer.fThetaMin = fTheta1;
buffer.fThetaMax = fTheta2;
buffer.fPhiMin = fPhi1;
buffer.fPhiMax = fPhi2;
buffer.SetSectionsValid(TBuffer3D::kShapeSpecific);
}
if (reqSections & TBuffer3D::kRawSizes) {
// We want FillBuffer to be const
TGeoSphere * localThis = const_cast<TGeoSphere *>(this);
localThis->SetNumberOfDivisions(gGeoManager->GetNsegments());
Int_t n = GetNumberOfDivisions()+1;
Int_t nz = GetNz()+1;
Int_t NbPnts = 2*n*nz;
if (nz < 2 || NbPnts <= 0) {
assert(kFALSE);
}
else {
Bool_t specialCase = (TMath::Abs(TMath::Sin(2*(fPhi2 - fPhi1))) <= 0.01);
Int_t NbSegs = 4*(nz*n-1+(specialCase == kTRUE));
Int_t NbPols = 2*(nz*n-1+(specialCase == kTRUE));
if (buffer.SetRawSizes(NbPnts, 3*NbPnts, NbSegs, 3*NbSegs, NbPols, 6*NbPols)) {
buffer.SetSectionsValid(TBuffer3D::kRawSizes);
}
}
}
if ((reqSections & TBuffer3D::kRaw) && buffer.SectionsValid(TBuffer3D::kRawSizes)) {
SetPoints(buffer.fPnts);
if (!buffer.fLocalFrame) {
TransformPoints(buffer.fPnts, buffer.NbPnts());
}
SetSegsAndPols(buffer);
buffer.SetSectionsValid(TBuffer3D::kRaw);
}
return buffer;
}
*/
//
#include "Riostream.h"
#include "TROOT.h"
#include "TGeoCone.h"
#include "TGeoManager.h"
#include "TGeoVolume.h"
#include "TVirtualGeoPainter.h"
#include "TGeoSphere.h"
#include "TVirtualPad.h"
#include "TBuffer3D.h"
#include "TBuffer3DTypes.h"
ClassImp(TGeoSphere)
//_____________________________________________________________________________
TGeoSphere::TGeoSphere()
{
// Default constructor
SetShapeBit(TGeoShape::kGeoSph);
fNz = 0;
fNseg = 0;
fRmin = 0.0;
fRmax = 0.0;
fTheta1 = 0.0;
fTheta2 = 180.0;
fPhi1 = 0.0;
fPhi2 = 360.0;
}
//_____________________________________________________________________________
TGeoSphere::TGeoSphere(Double_t rmin, Double_t rmax, Double_t theta1,
Double_t theta2, Double_t phi1, Double_t phi2)
:TGeoBBox(0, 0, 0)
{
// Default constructor specifying minimum and maximum radius
SetShapeBit(TGeoShape::kGeoSph);
SetSphDimensions(rmin, rmax, theta1, theta2, phi1, phi2);
ComputeBBox();
SetNumberOfDivisions(20);
}
//_____________________________________________________________________________
TGeoSphere::TGeoSphere(const char *name, Double_t rmin, Double_t rmax, Double_t theta1,
Double_t theta2, Double_t phi1, Double_t phi2)
:TGeoBBox(name, 0, 0, 0)
{
// Default constructor specifying minimum and maximum radius
SetShapeBit(TGeoShape::kGeoSph);
SetSphDimensions(rmin, rmax, theta1, theta2, phi1, phi2);
ComputeBBox();
SetNumberOfDivisions(20);
}
//_____________________________________________________________________________
TGeoSphere::TGeoSphere(Double_t *param, Int_t /*nparam*/)
:TGeoBBox(0, 0, 0)
{
// Default constructor specifying minimum and maximum radius
// param[0] = Rmin
// param[1] = Rmax
SetShapeBit(TGeoShape::kGeoSph);
SetDimensions(param);
ComputeBBox();
SetNumberOfDivisions(20);
}
//_____________________________________________________________________________
TGeoSphere::~TGeoSphere()
{
// destructor
}
//_____________________________________________________________________________
void TGeoSphere::ComputeBBox()
{
// compute bounding box of the sphere
// Double_t xmin, xmax, ymin, ymax, zmin, zmax;
if (TMath::Abs(fTheta2-fTheta1) == 180) {
if (TMath::Abs(fPhi2-fPhi1) == 360) {
TGeoBBox::SetBoxDimensions(fRmax, fRmax, fRmax);
memset(fOrigin, 0, 3*sizeof(Double_t));
return;
}
}
Double_t st1 = TMath::Sin(fTheta1*TMath::DegToRad());
Double_t st2 = TMath::Sin(fTheta2*TMath::DegToRad());
Double_t r1min, r1max, r2min, r2max, rmin, rmax;
r1min = TMath::Min(fRmax*st1, fRmax*st2);
r1max = TMath::Max(fRmax*st1, fRmax*st2);
r2min = TMath::Min(fRmin*st1, fRmin*st2);
r2max = TMath::Max(fRmin*st1, fRmin*st2);
if (((fTheta1<=90) && (fTheta2>=90)) || ((fTheta2<=90) && (fTheta1>=90))) {
r1max = fRmax;
r2max = fRmin;
}
rmin = TMath::Min(r1min, r2min);
rmax = TMath::Max(r1max, r2max);
Double_t xc[4];
Double_t yc[4];
xc[0] = rmax*TMath::Cos(fPhi1*TMath::DegToRad());
yc[0] = rmax*TMath::Sin(fPhi1*TMath::DegToRad());
xc[1] = rmax*TMath::Cos(fPhi2*TMath::DegToRad());
yc[1] = rmax*TMath::Sin(fPhi2*TMath::DegToRad());
xc[2] = rmin*TMath::Cos(fPhi1*TMath::DegToRad());
yc[2] = rmin*TMath::Sin(fPhi1*TMath::DegToRad());
xc[3] = rmin*TMath::Cos(fPhi2*TMath::DegToRad());
yc[3] = rmin*TMath::Sin(fPhi2*TMath::DegToRad());
Double_t xmin = xc[TMath::LocMin(4, &xc[0])];
Double_t xmax = xc[TMath::LocMax(4, &xc[0])];
Double_t ymin = yc[TMath::LocMin(4, &yc[0])];
Double_t ymax = yc[TMath::LocMax(4, &yc[0])];
Double_t dp = fPhi2-fPhi1;
if (dp<0) dp+=360;
Double_t ddp = -fPhi1;
if (ddp<0) ddp+= 360;
if (ddp>360) ddp-=360;
if (ddp<=dp) xmax = rmax;
ddp = 90-fPhi1;
if (ddp<0) ddp+= 360;
if (ddp>360) ddp-=360;
if (ddp<=dp) ymax = rmax;
ddp = 180-fPhi1;
if (ddp<0) ddp+= 360;
if (ddp>360) ddp-=360;
if (ddp<=dp) xmin = -rmax;
ddp = 270-fPhi1;
if (ddp<0) ddp+= 360;
if (ddp>360) ddp-=360;
if (ddp<=dp) ymin = -rmax;
xc[0] = fRmax*TMath::Cos(fTheta1*TMath::DegToRad());
xc[1] = fRmax*TMath::Cos(fTheta2*TMath::DegToRad());
xc[2] = fRmin*TMath::Cos(fTheta1*TMath::DegToRad());
xc[3] = fRmin*TMath::Cos(fTheta2*TMath::DegToRad());
Double_t zmin = xc[TMath::LocMin(4, &xc[0])];
Double_t zmax = xc[TMath::LocMax(4, &xc[0])];
fOrigin[0] = (xmax+xmin)/2;
fOrigin[1] = (ymax+ymin)/2;
fOrigin[2] = (zmax+zmin)/2;;
fDX = (xmax-xmin)/2;
fDY = (ymax-ymin)/2;
fDZ = (zmax-zmin)/2;
}
//_____________________________________________________________________________
void TGeoSphere::ComputeNormal(Double_t *point, Double_t *dir, Double_t *norm)
{
// Compute normal to closest surface from POINT.
Double_t rxy2 = point[0]*point[0]+point[1]*point[1];
Double_t r2 = rxy2+point[2]*point[2];
Double_t r=TMath::Sqrt(r2);
Bool_t rzero=kFALSE;
if (r<=1E-20) rzero=kTRUE;
//localize theta
Double_t phi=0;
Double_t th=0.;
if (!rzero) th = TMath::ACos(point[2]/r);
//localize phi
phi=TMath::ATan2(point[1], point[0]);
Double_t saf[4];
saf[0]=(fRmin==0 && !TestShapeBit(kGeoThetaSeg) && !TestShapeBit(kGeoPhiSeg))?TGeoShape::Big():TMath::Abs(r-fRmin);
saf[1]=TMath::Abs(fRmax-r);
saf[2]=saf[3]= TGeoShape::Big();
if (TestShapeBit(kGeoThetaSeg)) {
if (fTheta1>0) {
saf[2] = r*TMath::Abs(TMath::Sin(th-fTheta1*TMath::DegToRad()));
}
if (fTheta2<180) {
saf[3] = r*TMath::Abs(TMath::Sin(fTheta2*TMath::DegToRad()-th));
}
}
Int_t i = TMath::LocMin(4,saf);
if (TestShapeBit(kGeoPhiSeg)) {
Double_t c1 = TMath::Cos(fPhi1*TMath::DegToRad());
Double_t s1 = TMath::Sin(fPhi1*TMath::DegToRad());
Double_t c2 = TMath::Cos(fPhi2*TMath::DegToRad());
Double_t s2 = TMath::Sin(fPhi2*TMath::DegToRad());
if (TGeoShape::IsCloseToPhi(saf[i], point,c1,s1,c2,s2)) {
TGeoShape::NormalPhi(point,dir,norm,c1,s1,c2,s2);
return;
}
}
if (i>1) {
if (i==2) th=(fTheta1<90)?(fTheta1+90):(fTheta1-90);
else th=(fTheta2<90)?(fTheta2+90):(fTheta2-90);
th *= TMath::DegToRad();
}
norm[0] = TMath::Sin(th)*TMath::Cos(phi);
norm[1] = TMath::Sin(th)*TMath::Sin(phi);
norm[2] = TMath::Cos(th);
if (norm[0]*dir[0]+norm[1]*dir[1]+norm[2]*dir[2]<0) {
norm[0] = -norm[0];
norm[1] = -norm[1];
norm[2] = -norm[2];
}
}
//_____________________________________________________________________________
Bool_t TGeoSphere::IsPointInside(Double_t *point, Bool_t checkR, Bool_t checkTh, Bool_t checkPh) const
{
Double_t r2 = point[0]*point[0]+point[1]*point[1]+point[2]*point[2];
if (checkR) {
if (TestShapeBit(kGeoRSeg) && (r2<fRmin*fRmin)) return kFALSE;
if (r2>fRmax*fRmax) return kFALSE;
}
if (r2<1E-20) return kTRUE;
if (checkPh && TestShapeBit(kGeoPhiSeg)) {
Double_t phi = TMath::ATan2(point[1], point[0]) * TMath::RadToDeg();
while (phi < fPhi1) phi+=360.;
Double_t dphi = fPhi2 -fPhi1;
Double_t ddp = phi - fPhi1;
if (ddp > dphi) return kFALSE;
}
if (checkTh && TestShapeBit(kGeoThetaSeg)) {
r2=TMath::Sqrt(r2);
// check theta range
Double_t theta = TMath::ACos(point[2]/r2)*TMath::RadToDeg();
if ((theta<fTheta1) || (theta>fTheta2)) return kFALSE;
}
return kTRUE;
}
//_____________________________________________________________________________
Bool_t TGeoSphere::Contains(Double_t *point) const
{
// test if point is inside this sphere
// check Rmin<=R<=Rmax
Double_t r2=point[0]*point[0]+point[1]*point[1]+point[2]*point[2];
if (TestShapeBit(kGeoRSeg) && (r2<fRmin*fRmin)) return kFALSE;
if (r2>fRmax*fRmax) return kFALSE;
if (r2<1E-20) return kTRUE;
// check phi range
if (TestShapeBit(kGeoPhiSeg)) {
Double_t phi = TMath::ATan2(point[1], point[0]) * TMath::RadToDeg();
if (phi < 0 ) phi+=360.;
Double_t dphi = fPhi2 -fPhi1;
if (dphi < 0) dphi+=360.;
Double_t ddp = phi - fPhi1;
if (ddp < 0) ddp += 360.;
if (ddp > dphi) return kFALSE;
}
if (TestShapeBit(kGeoThetaSeg)) {
r2=TMath::Sqrt(r2);
// check theta range
Double_t theta = TMath::ACos(point[2]/r2)*TMath::RadToDeg();
if ((theta<fTheta1) || (theta>fTheta2)) return kFALSE;
}
return kTRUE;
}
//_____________________________________________________________________________
Int_t TGeoSphere::DistancetoPrimitive(Int_t px, Int_t py)
{
// compute closest distance from point px,py to each corner
Int_t n = fNseg+1;
Int_t nz = fNz+1;
const Int_t numPoints = 2*n*nz;
return ShapeDistancetoPrimitive(numPoints, px, py);
}
//_____________________________________________________________________________
Double_t TGeoSphere::DistFromOutside(Double_t *point, Double_t *dir, Int_t iact, Double_t step, Double_t *safe) const
{
// compute distance from outside point to surface of the sphere
Double_t saf[6];
Double_t rxy2 = point[0]*point[0]+point[1]*point[1];
Double_t rxy = TMath::Sqrt(rxy2);
Double_t r2 = rxy2+point[2]*point[2];
Double_t r=TMath::Sqrt(r2);
Bool_t rzero=kFALSE;
Double_t phi=0;;
if (r<1E-20) rzero=kTRUE;
//localize theta
Double_t th=0.;
if (TestShapeBit(kGeoThetaSeg) && (!rzero)) {
th = TMath::ACos(point[2]/r)*TMath::RadToDeg();
}
//localize phi
if (TestShapeBit(kGeoPhiSeg)) {
phi=TMath::ATan2(point[1], point[0])*TMath::RadToDeg();
if (phi<0) phi+=360.;
}
if (iact<3 && safe) {
saf[0]=(r<fRmin)?fRmin-r:TGeoShape::Big();
saf[1]=(r>fRmax)?(r-fRmax):TGeoShape::Big();
saf[2]=saf[3]=saf[4]=saf[5]= TGeoShape::Big();
if (TestShapeBit(kGeoThetaSeg)) {
if (th < fTheta1) {
saf[2] = r*TMath::Sin((fTheta1-th)*TMath::DegToRad());
}
if (th > fTheta2) {
saf[3] = r*TMath::Sin((th-fTheta2)*TMath::DegToRad());
}
}
if (TestShapeBit(kGeoPhiSeg)) {
Double_t dph1=phi-fPhi1;
if (dph1<0) dph1+=360.;
if (dph1<=90.) saf[4]=rxy*TMath::Sin(dph1*TMath::DegToRad());
Double_t dph2=fPhi2-phi;
if (dph2<0) dph2+=360.;
if (dph2>90.) saf[5]=rxy*TMath::Sin(dph2*TMath::DegToRad());
}
*safe = saf[TMath::LocMin(6, &saf[0])];
if (iact==0) return TGeoShape::Big();
if (iact==1 && step<*safe) return TGeoShape::Big();
}
// compute distance to shape
Double_t snxt = TGeoShape::Big();
Double_t rdotn = point[0]*dir[0]+point[1]*dir[1]+point[2]*dir[2];
Bool_t fullsph = (!TestShapeBit(kGeoThetaSeg) && !TestShapeBit(kGeoPhiSeg))?kTRUE:kFALSE;
if (fullsph) {
Bool_t inrmax = kFALSE;
Bool_t inrmin = kFALSE;
if (r<=fRmax+TGeoShape::Tolerance()) inrmax = kTRUE;
if (r>=fRmin-TGeoShape::Tolerance()) inrmin = kTRUE;
if (inrmax && inrmin) {
if ((fRmax-r) < (r-fRmin)) {
// close to Rmax
if (rdotn>=0) return TGeoShape::Big();
return 0.0; // already in
}
// close to Rmin
if (fRmin==0.0 || rdotn>=0) return 0.0;
// check second crossing of Rmin
return DistToSphere(point, dir, fRmin, kFALSE, kFALSE);
}
}
// first check if any crossing at all
if (r>fRmax) {
Double_t b = rdotn;
Double_t c = r2-fRmax*fRmax;
Double_t d=b*b-c;
if (d<0) return TGeoShape::Big();
}
// do rmin, rmax, checking phi and theta ranges
if (r<fRmin) {
// check first cross of rmin
snxt = DistToSphere(point, dir, fRmin, kTRUE);
if (snxt<1E20) return snxt;
} else {
if (r>fRmax) {
// point outside rmax, check first cross of rmax
snxt = DistToSphere(point, dir, fRmax, kTRUE);
if (snxt<1E20) return snxt;
// now check first crossing of rmin
if (fRmin>0) {
snxt = DistToSphere(point, dir, fRmin, kTRUE);
// if this is outside range, check second crossing of rmin
if (snxt>1E20) {
snxt = DistToSphere(point, dir, fRmin, kTRUE, kFALSE);
if (snxt<1E20) return snxt;
}
}
} else {
// point between rmin and rmax, check first cross of rmin
snxt = DistToSphere(point, dir, fRmin, kTRUE);
// if this is outside range, check second crossing of rmin
if (snxt>1E20) {
snxt = DistToSphere(point, dir, fRmin, kTRUE, kFALSE);
if (snxt<1E20) return snxt;
}
}
}
// check theta conical surfaces
Double_t ptnew[3];
Double_t b,delta, znew;
Double_t st1=TGeoShape::Big(), st2=TGeoShape::Big();
if (TestShapeBit(kGeoThetaSeg)) {
if (fTheta1>0) {
if (fTheta1==90) {
// surface is a plane
if (point[2]*dir[2]<0) {
snxt = -point[2]/dir[2];
ptnew[0] = point[0]+snxt*dir[0];
ptnew[1] = point[1]+snxt*dir[1];
ptnew[2] = 0;
// check range
if (IsPointInside(&ptnew[0], kTRUE, kFALSE, kTRUE)) return snxt;
}
} else {
Double_t r1,r2,z1,z2,dz;
Double_t si = TMath::Sin(fTheta1*TMath::DegToRad());
Double_t ci = TMath::Cos(fTheta1*TMath::DegToRad());
if (ci>0) {
r1 = fRmin*si;
z1 = fRmin*ci;
r2 = fRmax*si;
z2 = fRmax*ci;
} else {
r1 = fRmax*si;
z1 = fRmax*ci;
r2 = fRmin*si;
z2 = fRmin*ci;
}
dz = 0.5*(z2-z1);
ptnew[0] = point[0];
ptnew[1] = point[1];
ptnew[2] = point[2]-0.5*(z1+z2);
if (TestShapeBit(kGeoPhiSeg)) {
st1 = TGeoConeSeg::DistToCons(point, dir, r1, z1, r2, z2, fPhi1, fPhi2);
} else {
TGeoCone::DistToCone(ptnew, dir, dz, r1, r2, b, delta);
if (delta>0) {
st1 = -b-delta;
znew = ptnew[2]+st1*dir[2];
if (st1<0 || TMath::Abs(znew)>0) {
st1 = -b+delta;
znew = ptnew[2]+st1*dir[2];
if (st1<0 || TMath::Abs(znew)>0) st1=TGeoShape::Big();
}
}
}
}
}
if (fTheta2<180) {
if (fTheta2==90) {
// surface is a plane
if (point[2]*dir[2]<0) {
snxt = -point[2]/dir[2];
ptnew[0] = point[0]+snxt*dir[0];
ptnew[1] = point[1]+snxt*dir[1];
ptnew[2] = 0;
// check range
if (IsPointInside(&ptnew[0], kTRUE, kFALSE, kTRUE)) return snxt;
}
} else {
Double_t r1,r2,z1,z2,dz;
Double_t si = TMath::Sin(fTheta2*TMath::DegToRad());
Double_t ci = TMath::Cos(fTheta2*TMath::DegToRad());
if (ci>0) {
r1 = fRmin*si;
z1 = fRmin*ci;
r2 = fRmax*si;
z2 = fRmax*ci;
} else {
r1 = fRmax*si;
z1 = fRmax*ci;
r2 = fRmin*si;
z2 = fRmin*ci;
}
dz = 0.5*(z2-z1);
ptnew[0] = point[0];
ptnew[1] = point[1];
ptnew[2] = point[2]-0.5*(z1+z2);
if (TestShapeBit(kGeoPhiSeg)) {
st2 = TGeoConeSeg::DistToCons(point, dir, r1, z1, r2, z2, fPhi1, fPhi2);
} else {
TGeoCone::DistToCone(ptnew, dir, dz, r1, r2, b, delta);
if (delta>0) {
st2 = -b-delta;
znew = ptnew[2]+st2*dir[2];
if (st2<0 || TMath::Abs(znew)>dz) {
st2 = -b+delta;
znew = ptnew[2]+st2*dir[2];
if (st2<0 || TMath::Abs(znew)>0) st2=TGeoShape::Big();
}
}
}
}
}
}
snxt = TMath::Min(st1, st2);
// if (snxt<1E20) return snxt;
if (TestShapeBit(kGeoPhiSeg)) {
Double_t s1 = TMath::Sin(fPhi1*TMath::DegToRad());
Double_t c1 = TMath::Cos(fPhi1*TMath::DegToRad());
Double_t s2 = TMath::Sin(fPhi2*TMath::DegToRad());
Double_t c2 = TMath::Cos(fPhi2*TMath::DegToRad());
Double_t phim = 0.5*(fPhi1+fPhi2);
Double_t sm = TMath::Sin(phim*TMath::DegToRad());
Double_t cm = TMath::Cos(phim*TMath::DegToRad());
Double_t sfi1=TGeoShape::Big();
Double_t sfi2=TGeoShape::Big();
Double_t s=0;
Double_t safety, un;
safety = point[0]*s1-point[1]*c1;
if (safety>0) {
un = dir[0]*s1-dir[1]*c1;
if (un<0) {
s=-safety/un;
ptnew[0] = point[0]+s*dir[0];
ptnew[1] = point[1]+s*dir[1];
ptnew[2] = point[2]+s*dir[2];
if ((ptnew[1]*cm-ptnew[0]*sm)<=0) {
sfi1=s;
if (IsPointInside(&ptnew[0], kTRUE, kTRUE, kFALSE) && sfi1<snxt) return sfi1;
}
}
}
safety = -point[0]*s2+point[1]*c2;
if (safety>0) {
un = -dir[0]*s2+dir[1]*c2;
if (un<0) {
s=-safety/un;
ptnew[0] = point[0]+s*dir[0];
ptnew[1] = point[1]+s*dir[1];
ptnew[2] = point[2]+s*dir[2];
if ((ptnew[1]*cm-ptnew[0]*sm)>=0) {
sfi2=s;
if (IsPointInside(&ptnew[0], kTRUE, kTRUE, kFALSE) && sfi2<snxt) return sfi2;
}
}
}
}
return snxt;
}
//_____________________________________________________________________________
Double_t TGeoSphere::DistFromInside(Double_t *point, Double_t *dir, Int_t iact, Double_t step, Double_t *safe) const
{
// compute distance from inside point to surface of the sphere
Double_t saf[6];
Double_t rxy2 = point[0]*point[0]+point[1]*point[1];
Double_t rxy = TMath::Sqrt(rxy2);
Double_t r2 = rxy2+point[2]*point[2];
Double_t r=TMath::Sqrt(r2);
Bool_t rzero=kFALSE;
if (r<=1E-20) rzero=kTRUE;
//localize theta
Double_t phi=0;;
Double_t th=0.;
if (TestShapeBit(kGeoThetaSeg) && (!rzero)) {
th = TMath::ACos(point[2]/r)*TMath::RadToDeg();
}
//localize phi
if (TestShapeBit(kGeoPhiSeg)) {
phi=TMath::ATan2(point[1], point[0])*TMath::RadToDeg();
if (phi<0) phi+=360.;
}
if (iact<3 && safe) {
saf[0]=(fRmin==0)?TGeoShape::Big():r-fRmin;
saf[1]=fRmax-r;
saf[2]=saf[3]=saf[4]=saf[5]= TGeoShape::Big();
if (TestShapeBit(kGeoThetaSeg)) {
if (fTheta1>0) {
saf[2] = r*TMath::Sin((th-fTheta1)*TMath::DegToRad());
}
if (fTheta2<180) {
saf[3] = r*TMath::Sin((fTheta2-th)*TMath::DegToRad());
}
}
if (TestShapeBit(kGeoPhiSeg)) {
Double_t dph1=phi-fPhi1;
if (dph1<0) dph1+=360.;
if (dph1<=90.) saf[4]=rxy*TMath::Sin(dph1*TMath::DegToRad());
Double_t dph2=fPhi2-phi;
if (dph2<0) dph2+=360.;
if (dph2<=90.) saf[5]=rxy*TMath::Sin(dph2*TMath::DegToRad());
}
*safe = saf[TMath::LocMin(6, &saf[0])];
if (iact==0) return TGeoShape::Big();
if (iact==1 && step<*safe) return TGeoShape::Big();
}
// compute distance to shape
Double_t snxt = TGeoShape::Big();
if (rzero) {
// gGeoManager->SetNormalChecked(1.);
return fRmax;
}
// first do rmin, rmax
Double_t b,delta, znew;
Double_t rdotn = point[0]*dir[0]+point[1]*dir[1]+point[2]*dir[2];
Double_t sn1 = TGeoShape::Big();
// Inner sphere
if (fRmin>0) {
// Protection in case point is actually outside the sphere
if (r <= fRmin+TGeoShape::Tolerance()) {
if (rdotn<0) return 0.0;
} else {
if (rdotn<0) sn1 = DistToSphere(point, dir, fRmin, kFALSE);
}
}
Double_t sn2 = TGeoShape::Big();
// Outer sphere
if (r >= fRmax-TGeoShape::Tolerance()) {
if (rdotn>=0) return 0.0;
}
sn2 = DistToSphere(point, dir, fRmax, kFALSE);
Double_t sr = TMath::Min(sn1, sn2);
// check theta conical surfaces
sn1 = TGeoShape::Big();
sn2 = TGeoShape::Big();
if (TestShapeBit(kGeoThetaSeg)) {
if (fTheta1==90) {
// surface is a plane
if (point[2]*dir[2]<0) sn1 = -point[2]/dir[2];
} else {
if (fTheta1>0) {
Double_t r1,r2,z1,z2,dz,ptnew[3];
Double_t si = TMath::Sin(fTheta1*TMath::DegToRad());
Double_t ci = TMath::Cos(fTheta1*TMath::DegToRad());
if (ci>0) {
r1 = fRmin*si;
z1 = fRmin*ci;
r2 = fRmax*si;
z2 = fRmax*ci;
} else {
r1 = fRmax*si;
z1 = fRmax*ci;
r2 = fRmin*si;
z2 = fRmin*ci;
}
dz = 0.5*(z2-z1);
ptnew[0] = point[0];
ptnew[1] = point[1];
ptnew[2] = point[2]-0.5*(z1+z2);
if (TestShapeBit(kGeoPhiSeg)) {
sn1 = TGeoConeSeg::DistToCons(point, dir, r1, z1, r2, z2, fPhi1, fPhi2);
} else {
TGeoCone::DistToCone(ptnew, dir, dz, r1, r2, b, delta);
if (delta>0) {
sn1 = -b-delta;
znew = ptnew[2]+sn1*dir[2];
if (sn1<0 || TMath::Abs(znew)>dz) {
sn1 = -b+delta;
znew = ptnew[2]+sn1*dir[2];
if (sn1<0 || TMath::Abs(znew)>0) sn1=TGeoShape::Big();
}
}
}
}
}
if (fTheta2==90) {
// surface is a plane
if (point[2]*dir[2]<0) sn1 = -point[2]/dir[2];
} else {
if (fTheta2<180) {
Double_t r1,r2,z1,z2,dz,ptnew[3];
Double_t si = TMath::Sin(fTheta2*TMath::DegToRad());
Double_t ci = TMath::Cos(fTheta2*TMath::DegToRad());
if (ci>0) {
r1 = fRmin*si;
z1 = fRmin*ci;
r2 = fRmax*si;
z2 = fRmax*ci;
} else {
r1 = fRmax*si;
z1 = fRmax*ci;
r2 = fRmin*si;
z2 = fRmin*ci;
}
dz = 0.5*(z2-z1);
ptnew[0] = point[0];
ptnew[1] = point[1];
ptnew[2] = point[2]-0.5*(z1+z2);
if (TestShapeBit(kGeoPhiSeg)) {
sn2 = TGeoConeSeg::DistToCons(point, dir, r1, z1, r2, z2, fPhi1, fPhi2);
} else {
TGeoCone::DistToCone(ptnew, dir, dz, r1, r2, b, delta);
if (delta>0) {
sn2 = -b-delta;
znew = ptnew[2]+sn2*dir[2];
if (sn2<0 || TMath::Abs(znew)>0) {
sn2 = -b+delta;
znew = ptnew[2]+sn2*dir[2];
if (sn2<0 || TMath::Abs(znew)>0) sn2=TGeoShape::Big();
}
}
}
}
}
}
Double_t st = TMath::Min(sn1,sn2);
Double_t sp = TGeoShape::Big();
if (TestShapeBit(kGeoPhiSeg)) {
Double_t s1 = TMath::Sin(fPhi1*TMath::DegToRad());
Double_t c1 = TMath::Cos(fPhi1*TMath::DegToRad());
Double_t s2 = TMath::Sin(fPhi2*TMath::DegToRad());
Double_t c2 = TMath::Cos(fPhi2*TMath::DegToRad());
Double_t phim = 0.5*(fPhi1+fPhi2);
Double_t sm = TMath::Sin(phim*TMath::DegToRad());
Double_t cm = TMath::Cos(phim*TMath::DegToRad());
sp = TGeoShape::DistToPhiMin(point, dir, s1, c1, s2, c2, sm, cm);
}
snxt = TMath::Min(sr, st);
snxt = TMath::Min(snxt, sp);
return snxt;
}
//_____________________________________________________________________________
Double_t TGeoSphere::DistToSphere(Double_t *point, Double_t *dir, Double_t rsph, Bool_t check, Bool_t firstcross) const
{
// compute distance to sphere of radius rsph. Direction has to be a unit vector
if (rsph<=0) return TGeoShape::Big();
Double_t s=TGeoShape::Big();
Double_t r2 = point[0]*point[0]+point[1]*point[1]+point[2]*point[2];
Double_t b = point[0]*dir[0]+point[1]*dir[1]+point[2]*dir[2];
Double_t c = r2-rsph*rsph;
Bool_t in = (c<=0)?kTRUE:kFALSE;
Double_t d;
d=b*b-c;
if (d<0) return TGeoShape::Big();
Double_t pt[3];
Int_t i;
d = TMath::Sqrt(d);
if (in) {
s=-b+d;
} else {
s = (firstcross)?(-b-d):(-b+d);
}
if (s<0) return TGeoShape::Big();
if (!check) return s;
for (i=0; i<3; i++) pt[i]=point[i]+s*dir[i];
// check theta and phi ranges
if (IsPointInside(&pt[0], kFALSE)) return s;
return TGeoShape::Big();
}
//_____________________________________________________________________________
TGeoVolume *TGeoSphere::Divide(TGeoVolume * /*voldiv*/, const char * /*divname*/, Int_t /*iaxis*/, Int_t /*ndiv*/,
Double_t /*start*/, Double_t /*step*/)
{
// Divide all range of iaxis in range/step cells
Error("Divide", "Division of a sphere not implemented");
return 0;
}
//_____________________________________________________________________________
const char *TGeoSphere::GetAxisName(Int_t iaxis) const
{
// Returns name of axis IAXIS.
switch (iaxis) {
case 1:
return "R";
case 2:
return "THETA";
case 3:
return "PHI";
default:
return "UNDEFINED";
}
}
//_____________________________________________________________________________
Double_t TGeoSphere::GetAxisRange(Int_t iaxis, Double_t &xlo, Double_t &xhi) const
{
// Get range of shape for a given axis.
xlo = 0;
xhi = 0;
Double_t dx = 0;
switch (iaxis) {
case 1:
xlo = fRmin;
xhi = fRmax;
dx = xhi-xlo;
return dx;
case 2:
xlo = fPhi1;
xhi = fPhi2;
dx = xhi-xlo;
return dx;
case 3:
xlo = fTheta1;
xhi = fTheta2;
dx = xhi-xlo;
return dx;
}
return dx;
}
//_____________________________________________________________________________
void TGeoSphere::GetBoundingCylinder(Double_t *param) const
{
//--- Fill vector param[4] with the bounding cylinder parameters. The order
// is the following : Rmin, Rmax, Phi1, Phi2
Double_t smin = TMath::Sin(fTheta1*TMath::DegToRad());
Double_t smax = TMath::Sin(fTheta2*TMath::DegToRad());
if (smin>smax) {
Double_t a = smin;
smin = smax;
smax = a;
}
param[0] = fRmin*smin; // Rmin
param[0] *= param[0];
if (((90.-fTheta1)*(fTheta2-90.))>=0) smax = 1.;
param[1] = fRmax*smax; // Rmax
param[1] *= param[1];
param[2] = (fPhi1<0)?(fPhi1+360.):fPhi1; // Phi1
param[3] = fPhi2;
if ((param[3]-param[2])==360.) { // Phi2
param[2] = 0.;
param[3] = 360.;
}
while (param[3]<param[2]) param[3]+=360.;
}
//_____________________________________________________________________________
void TGeoSphere::InspectShape() const
{
// print shape parameters
printf("*** Shape %s: TGeoSphere ***\n", GetName());
printf(" Rmin = %11.5f\n", fRmin);
printf(" Rmax = %11.5f\n", fRmax);
printf(" Th1 = %11.5f\n", fTheta1);
printf(" Th2 = %11.5f\n", fTheta2);
printf(" Ph1 = %11.5f\n", fPhi1);
printf(" Ph2 = %11.5f\n", fPhi2);
printf(" Bounding box:\n");
TGeoBBox::InspectShape();
}
//_____________________________________________________________________________
TBuffer3D *TGeoSphere::MakeBuffer3D() const
{
// Creates a TBuffer3D describing *this* shape.
// Coordinates are in local reference frame.
Int_t n = gGeoManager->GetNsegments()+1;
Double_t ph1 = GetPhi1();
Double_t ph2 = GetPhi2();
Int_t nz = GetNz()+1;
if (nz < 2) return 0;
Int_t NbPnts = 2*n*nz;
if (NbPnts <= 0) return 0;
Bool_t specialCase = kFALSE;
if (TMath::Abs(TMath::Sin(2*(ph2 - ph1))) <= 0.01) specialCase = kTRUE;
Int_t NbSegs = 4*(nz*n-1+(specialCase == kTRUE));
Int_t NbPols = 2*(nz*n-1+(specialCase == kTRUE));
TBuffer3D* buff = new TBuffer3D(TBuffer3DTypes::kGeneric,
NbPnts, 3*NbPnts, NbSegs, 3*NbSegs, NbPols, 6*NbPols);
if (buff)
{
SetPoints(buff->fPnts);
SetSegsAndPols(*buff);
}
return buff;
}
//_____________________________________________________________________________
void TGeoSphere::SetSegsAndPols(TBuffer3D & buff) const
{
// Fill TBuffer3D structure for segments and polygons.
Int_t i, j;
Int_t n = gGeoManager->GetNsegments()+1;
Double_t ph1 = GetPhi1();
Double_t ph2 = GetPhi2();
Int_t nz = GetNz()+1;
if (nz < 2) return;
Bool_t specialCase = kFALSE;
if (TMath::Abs(TMath::Sin(2*(ph2 - ph1))) <= 0.01) specialCase = kTRUE;
Int_t c = GetBasicColor();
Int_t indx, indx2, k;
indx = indx2 = 0;
//inside & outside spheres, number of segments: 2*nz*(n-1)
// special case number of segments: 2*nz*n
for (i = 0; i < nz*2; i++) {
indx2 = i*n;
for (j = 1; j < n; j++) {
buff.fSegs[indx++] = c;
buff.fSegs[indx++] = indx2+j-1;
buff.fSegs[indx++] = indx2+j;
}
if (specialCase) {
buff.fSegs[indx++] = c;
buff.fSegs[indx++] = indx2+j-1;
buff.fSegs[indx++] = indx2;
}
}
//bottom & top lines, number of segments: 2*n
for (i = 0; i < 2; i++) {
indx2 = i*(nz-1)*2*n;
for (j = 0; j < n; j++) {
buff.fSegs[indx++] = c;
buff.fSegs[indx++] = indx2+j;
buff.fSegs[indx++] = indx2+n+j;
}
}
//inside & outside spheres, number of segments: 2*(nz-1)*n
for (i = 0; i < (nz-1); i++) {
//inside sphere
indx2 = i*n*2;
for (j = 0; j < n; j++) {
buff.fSegs[indx++] = c+2;
buff.fSegs[indx++] = indx2+j;
buff.fSegs[indx++] = indx2+n*2+j;
}
//outside sphere
indx2 = i*n*2+n;
for (j = 0; j < n; j++) {
buff.fSegs[indx++] = c+3;
buff.fSegs[indx++] = indx2+j;
buff.fSegs[indx++] = indx2+n*2+j;
}
}
//left & right sections, number of segments: 2*(nz-2)
// special case number of segments: 0
if (!specialCase) {
for (i = 1; i < (nz-1); i++) {
for (j = 0; j < 2; j++) {
buff.fSegs[indx++] = c;
buff.fSegs[indx++] = 2*i * n + j*(n-1);
buff.fSegs[indx++] = (2*i+1) * n + j*(n-1);
}
}
}
Int_t m = n - 1 + (specialCase == kTRUE);
indx = 0;
//bottom & top, number of polygons: 2*(n-1)
// special case number of polygons: 2*n
i = 0;
for (j = 0; j < n-1; j++) {
buff.fPols[indx++] = c+3;
buff.fPols[indx++] = 4;
buff.fPols[indx++] = i*(nz*2-2)*m+j;
buff.fPols[indx++] = 2*nz*m+i*n+j+1;
buff.fPols[indx++] = i*(nz*2-2)*m+m+j;
buff.fPols[indx++] = 2*nz*m+i*n+j;
}
if (specialCase) {
buff.fPols[indx++] = c+3;
buff.fPols[indx++] = 4;
buff.fPols[indx++] = i*(nz*2-2)*m+j;
buff.fPols[indx++] = 2*nz*m+i*n;
buff.fPols[indx++] = i*(nz*2-2)*m+m+j;
buff.fPols[indx++] = 2*nz*m+i*n+j;
}
i = 1;
for (j = 0; j < n-1; j++) {
buff.fPols[indx++] = c+3;
buff.fPols[indx++] = 4;
buff.fPols[indx++] = 2*nz*m+i*n+j;
buff.fPols[indx++] = i*(nz*2-2)*m+m+j;
buff.fPols[indx++] = 2*nz*m+i*n+j+1;
buff.fPols[indx++] = i*(nz*2-2)*m+j;
}
if (specialCase) {
buff.fPols[indx++] = c+3;
buff.fPols[indx++] = 4;
buff.fPols[indx++] = 2*nz*m+i*n+j;
buff.fPols[indx++] = i*(nz*2-2)*m+m+j;
buff.fPols[indx++] = 2*nz*m+i*n;
buff.fPols[indx++] = i*(nz*2-2)*m+j;
}
//inside & outside, number of polygons: (nz-1)*2*(n-1)
for (k = 0; k < (nz-1); k++) {
i = 0;
for (j = 0; j < n-1; j++) {
buff.fPols[indx++] = c+i;
buff.fPols[indx++] = 4;
buff.fPols[indx++] = (2*k+i*1)*m+j;
buff.fPols[indx++] = nz*2*m+(2*k+i*1+2)*n+j;
buff.fPols[indx++] = (2*k+i*1+2)*m+j;
buff.fPols[indx++] = nz*2*m+(2*k+i*1+2)*n+j+1;
}
if (specialCase) {
buff.fPols[indx++] = c+i;
buff.fPols[indx++] = 4;
buff.fPols[indx++] = (2*k+i*1)*m+j;
buff.fPols[indx++] = nz*2*m+(2*k+i*1+2)*n+j;
buff.fPols[indx++] = (2*k+i*1+2)*m+j;
buff.fPols[indx++] = nz*2*m+(2*k+i*1+2)*n;
}
i = 1;
for (j = 0; j < n-1; j++) {
buff.fPols[indx++] = c+i;
buff.fPols[indx++] = 4;
buff.fPols[indx++] = nz*2*m+(2*k+i*1+2)*n+j+1;
buff.fPols[indx++] = (2*k+i*1+2)*m+j;
buff.fPols[indx++] = nz*2*m+(2*k+i*1+2)*n+j;
buff.fPols[indx++] = (2*k+i*1)*m+j;
}
if (specialCase) {
buff.fPols[indx++] = c+i;
buff.fPols[indx++] = 4;
buff.fPols[indx++] = nz*2*m+(2*k+i*1+2)*n;
buff.fPols[indx++] = (2*k+i*1+2)*m+j;
buff.fPols[indx++] = nz*2*m+(2*k+i*1+2)*n+j;
buff.fPols[indx++] = (2*k+i*1)*m+j;
}
}
//left & right sections, number of polygons: 2*(nz-1)
// special case number of polygons: 0
if (!specialCase) {
indx2 = nz*2*(n-1);
for (k = 0; k < (nz-1); k++) {
i = 0;
buff.fPols[indx++] = c+2;
buff.fPols[indx++] = 4;
buff.fPols[indx++] = k==0 ? indx2+i*(n-1) : indx2+2*nz*n+2*(k-1)+i;
buff.fPols[indx++] = indx2+(2*k+3)*n+i*(n-1);
buff.fPols[indx++] = indx2+2*nz*n+2*k+i;
buff.fPols[indx++] = indx2+2*(k+1)*n+i*(n-1);
i = 1;
buff.fPols[indx++] = c+2;
buff.fPols[indx++] = 4;
buff.fPols[indx++] = k==0 ? indx2+i*(n-1) : indx2+2*nz*n+2*(k-1)+i;
buff.fPols[indx++] = indx2+2*(k+1)*n+i*(n-1);
buff.fPols[indx++] = indx2+2*nz*n+2*k+i;
buff.fPols[indx++] = indx2+(2*k+3)*n+i*(n-1);
}
buff.fPols[indx-8] = indx2+n;
buff.fPols[indx-2] = indx2+2*n-1;
}
}
//_____________________________________________________________________________
Double_t TGeoSphere::Safety(Double_t *point, Bool_t in) const
{
// computes the closest distance from given point to this shape, according
// to option. The matching point on the shape is stored in spoint.
Double_t r2 = point[0]*point[0]+point[1]*point[1]+point[2]*point[2];
Double_t r=TMath::Sqrt(r2);
Bool_t rzero=kFALSE;
if (r<=1E-20) rzero=kTRUE;
//localize theta
Double_t th=0.;
if (TestShapeBit(kGeoThetaSeg) && (!rzero)) {
th = TMath::ACos(point[2]/r)*TMath::RadToDeg();
}
Double_t saf[4];
saf[0]=(fRmin==0 && !TestShapeBit(kGeoThetaSeg) && !TestShapeBit(kGeoPhiSeg))?TGeoShape::Big():r-fRmin;
saf[1]=fRmax-r;
saf[2]=saf[3]= TGeoShape::Big();
if (TestShapeBit(kGeoThetaSeg)) {
if (fTheta1>0) saf[2] = r*TMath::Sin((th-fTheta1)*TMath::DegToRad());
if (fTheta2<180) saf[3] = r*TMath::Sin((fTheta2-th)*TMath::DegToRad());
}
Double_t safphi = TGeoShape::Big();
Double_t safe = TGeoShape::Big();
if (TestShapeBit(kGeoPhiSeg)) safphi = TGeoShape::SafetyPhi(point,in,fPhi1,fPhi2);
if (in) {
safe = saf[TMath::LocMin(4,saf)];
return TMath::Min(safe,safphi);
}
for (Int_t i=0; i<4; i++) saf[i]=-saf[i];
safe = saf[TMath::LocMax(4, saf)];
if (TestShapeBit(kGeoPhiSeg)) return TMath::Max(safe, safphi);
return safe;
}
//_____________________________________________________________________________
void TGeoSphere::SavePrimitive(ofstream &out, Option_t * /*option*/)
{
// Save a primitive as a C++ statement(s) on output stream "out".
if (TObject::TestBit(kGeoSavePrimitive)) return;
out << " // Shape: " << GetName() << " type: " << ClassName() << endl;
out << " rmin = " << fRmin << ";" << endl;
out << " rmax = " << fRmax << ";" << endl;
out << " theta1 = " << fTheta1<< ";" << endl;
out << " theta2 = " << fTheta2 << ";" << endl;
out << " phi1 = " << fPhi1 << ";" << endl;
out << " phi2 = " << fPhi2 << ";" << endl;
out << " TGeoShape *" << GetPointerName() << " = new TGeoSphere(\"" << GetName() << "\",rmin,rmax,theta1, theta2,phi1,phi2);" << endl;
TObject::SetBit(TGeoShape::kGeoSavePrimitive);
}
//_____________________________________________________________________________
void TGeoSphere::SetSphDimensions(Double_t rmin, Double_t rmax, Double_t theta1,
Double_t theta2, Double_t phi1, Double_t phi2)
{
if (rmin >= rmax) {
Error("SetDimensions", "invalid parameters rmin/rmax");
return;
}
fRmin = rmin;
fRmax = rmax;
if (rmin>0) SetShapeBit(kGeoRSeg);
if (theta1 >= theta2 || theta1<0 || theta1>180 || theta2>180) {
Error("SetDimensions", "invalid parameters theta1/theta2");
return;
}
fTheta1 = theta1;
fTheta2 = theta2;
if ((theta2-theta1)<180.) SetShapeBit(kGeoThetaSeg);
fPhi1 = phi1;
if (phi1<0) fPhi1+=360.;
fPhi2 = phi2;
while (fPhi2<fPhi1) fPhi2+=360.;
if (TMath::Abs(phi2-phi1)!=360.) SetShapeBit(kGeoPhiSeg);
}
//_____________________________________________________________________________
void TGeoSphere::SetDimensions(Double_t *param)
{
Double_t rmin = param[0];
Double_t rmax = param[1];
Double_t theta1 = 0;
Double_t theta2 = 180.;
Double_t phi1 = 0;
Double_t phi2 = 360.;
// if (nparam > 2) theta1 = param[2];
// if (nparam > 3) theta2 = param[3];
// if (nparam > 4) phi1 = param[4];
// if (nparam > 5) phi2 = param[5];
SetSphDimensions(rmin, rmax, theta1, theta2, phi1, phi2);
}
//_____________________________________________________________________________
void TGeoSphere::SetNumberOfDivisions(Int_t p)
{
fNseg = p;
Double_t dphi = fPhi2 - fPhi1;
if (dphi<0) dphi+=360;
Double_t dtheta = TMath::Abs(fTheta2-fTheta1);
fNz = Int_t(fNseg*dtheta/dphi) +1;
}
//_____________________________________________________________________________
void TGeoSphere::SetPoints(Double_t *points) const
{
// create sphere mesh points
Int_t i,j ;
if (points) {
Double_t dphi = fPhi2-fPhi1;
if (dphi<0) dphi+=360;
Double_t dtheta = fTheta2-fTheta1;
Int_t n = fNseg + 1;
dphi = dphi/fNseg;
dtheta = dtheta/fNz;
Double_t z, theta, phi, cphi, sphi;
Int_t indx=0;
for (i = 0; i < fNz+1; i++)
{
theta = (fTheta1+i*dtheta)*TMath::DegToRad();
z = fRmin * TMath::Cos(theta); // fSinPhiTab[i];
Double_t zi = fRmin*TMath::Sin(theta);
// printf("plane %i nseg=%i z=%f:\n", i,n,z);
for (j = 0; j < n; j++) {
phi = (fPhi1+j*dphi)*TMath::DegToRad();
cphi = TMath::Cos(phi);
sphi = TMath::Sin(phi);
points[indx++] = zi * cphi;
points[indx++] = zi * sphi;
points[indx++] = z;
// printf("%i %f %f %f\n", j, points[3*j], points[3*j+1], points[3*j+2]);
}
z = fRmax * TMath::Cos(theta);
zi = fRmax* TMath::Sin(theta);
// printf("outer points for plane %i:\n", i);
for (j = 0; j < n; j++) {
phi = (fPhi1+j*dphi)*TMath::DegToRad();
cphi = TMath::Cos(phi);
sphi = TMath::Sin(phi);
points[indx++] = zi * cphi;
points[indx++] = zi * sphi;
points[indx++] = z;
// printf("%i %f %f %f\n", j, points[n+3*j], points[n+3*j+1], points[n+3*j+2]);
}
}
}
}
//_____________________________________________________________________________
void TGeoSphere::SetPoints(Float_t *points) const
{
// create sphere mesh points
Int_t i,j ;
if (points) {
Double_t dphi = fPhi2-fPhi1;
if (dphi<0) dphi+=360;
Double_t dtheta = fTheta2-fTheta1;
Int_t n = fNseg + 1;
dphi = dphi/fNseg;
dtheta = dtheta/fNz;
Double_t z, theta, phi, cphi, sphi;
Int_t indx=0;
for (i = 0; i < fNz+1; i++)
{
theta = (fTheta1+i*dtheta)*TMath::DegToRad();
z = fRmin * TMath::Cos(theta); // fSinPhiTab[i];
Double_t zi = fRmin*TMath::Sin(theta);
// printf("plane %i nseg=%i z=%f:\n", i,n,z);
for (j = 0; j < n; j++)
{
phi = (fPhi1+j*dphi)*TMath::DegToRad();
cphi = TMath::Cos(phi);
sphi = TMath::Sin(phi);
points[indx++] = zi * cphi;
points[indx++] = zi * sphi;
points[indx++] = z;
// printf("%i %f %f %f\n", j, points[3*j], points[3*j+1], points[3*j+2]);
}
z = fRmax * TMath::Cos(theta);
zi = fRmax* TMath::Sin(theta);
// printf("outer points for plane %i:\n", i);
for (j = 0; j < n; j++)
{
phi = (fPhi1+j*dphi)*TMath::DegToRad();
cphi = TMath::Cos(phi);
sphi = TMath::Sin(phi);
points[indx++] = zi * cphi;
points[indx++] = zi * sphi;
points[indx++] = z;
// printf("%i %f %f %f\n", j, points[n+3*j], points[n+3*j+1], points[n+3*j+2]);
}
}
}
}
//_____________________________________________________________________________
Int_t TGeoSphere::GetNmeshVertices() const
{
// Return number of vertices of the mesh representation
Int_t n;
n = fNseg+1;
Int_t nz = fNz+1;
Int_t numPoints = 2*n*nz;
return numPoints;
}
//_____________________________________________________________________________
void TGeoSphere::Sizeof3D() const
{
///// fill size of this 3-D object
/// TVirtualGeoPainter *painter = gGeoManager->GetGeomPainter();
/// if (!painter) return;
///
/// Int_t n;
/// n = fNseg+1;
/// Int_t nz = fNz+1;
/// Bool_t specialCase = kFALSE;
///
/// if (TMath::Abs(TMath::Sin(2*(fPhi2 - fPhi1))) <= 0.01) //mark this as a very special case, when
/// specialCase = kTRUE; //we have to draw this PCON like a TUBE
///
/// Int_t numPoints = 2*n*nz;
/// Int_t numSegs = 4*(nz*n-1+(specialCase == kTRUE));
/// Int_t numPolys = 2*(nz*n-1+(specialCase == kTRUE));
/// painter->AddSize3D(numPoints, numSegs, numPolys);
}
const TBuffer3D & TGeoSphere::GetBuffer3D(Int_t reqSections, Bool_t localFrame) const
{
static TBuffer3DSphere buffer;
TGeoBBox::FillBuffer3D(buffer, reqSections, localFrame);
if (reqSections & TBuffer3D::kShapeSpecific) {
buffer.fRadiusInner = fRmin;
buffer.fRadiusOuter = fRmax;
buffer.fThetaMin = fTheta1;
buffer.fThetaMax = fTheta2;
buffer.fPhiMin = fPhi1;
buffer.fPhiMax = fPhi2;
buffer.SetSectionsValid(TBuffer3D::kShapeSpecific);
}
if (reqSections & TBuffer3D::kRawSizes) {
// We want FillBuffer to be const
TGeoSphere * localThis = const_cast<TGeoSphere *>(this);
localThis->SetNumberOfDivisions(gGeoManager->GetNsegments());
Int_t n = GetNumberOfDivisions()+1;
Int_t nz = GetNz()+1;
Int_t NbPnts = 2*n*nz;
if (nz < 2 || NbPnts <= 0) {
assert(kFALSE);
}
else {
Bool_t specialCase = (TMath::Abs(TMath::Sin(2*(fPhi2 - fPhi1))) <= 0.01);
Int_t NbSegs = 4*(nz*n-1+(specialCase == kTRUE));
Int_t NbPols = 2*(nz*n-1+(specialCase == kTRUE));
if (buffer.SetRawSizes(NbPnts, 3*NbPnts, NbSegs, 3*NbSegs, NbPols, 6*NbPols)) {
buffer.SetSectionsValid(TBuffer3D::kRawSizes);
}
}
}
if ((reqSections & TBuffer3D::kRaw) && buffer.SectionsValid(TBuffer3D::kRawSizes)) {
SetPoints(buffer.fPnts);
if (!buffer.fLocalFrame) {
TransformPoints(buffer.fPnts, buffer.NbPnts());
}
SetSegsAndPols(buffer);
buffer.SetSectionsValid(TBuffer3D::kRaw);
}
return buffer;
}