You may recall the Bragg law from your high school physics
giving the scattering condition for
a wave of wavelength 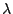 against a series of
lattice planes with lattice spacing
against a series of
lattice planes with lattice spacing 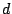 , rotated the angle
, rotated the angle 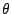 off the lattice plane normal.
off the lattice plane normal. 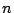 is an integer giving the spectral
order of the scattered wave. In neutron science one often refers to
the scattering vector,
is an integer giving the spectral
order of the scattered wave. In neutron science one often refers to
the scattering vector, 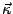 of a given reflection, where
of a given reflection, where
This gives us the scattering vector formulation of the Bragg law
where
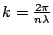 .
The Bragg law / scattering condition is illustrated in Figure 1.
.
The Bragg law / scattering condition is illustrated in Figure 1.
Figure 1:
Illustration of the Bragg Law.
|
|
Most of the neutron processes we will study in this paper are elastic,
meaning that the wavelength of the neutron is unaltered by the process.
Peter Willendrup
2005-11-16